Serie HF-Simulation - Teil 1 So funktioniert die numerische Modellierung von Antennen

In der Artikelreihe wird die simulationsgestützte Entwicklung von Antennen beleuchtet, von den Grundlagen numerischer Modellierung bis zur Optimierung und der effizienten Systembetrachtung.

Anbieter zum Thema

CADFEM Germany GmbH

CSA Group Bayern GmbH

MES Electronic Connect GmbH & Co. KG

Würth Elektronik eiSos GmbH & Co. KG

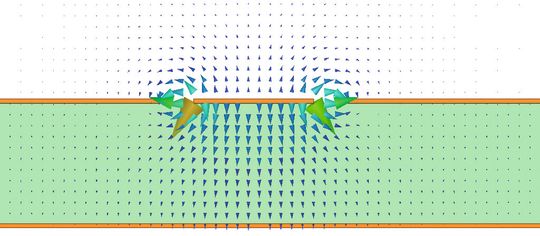
Simple Antennendesigns sind leicht zu realisieren. Sie sind jedoch nicht die Regel. Die erste und einfachste Antenne ist die Hertz’sche Dipolantenne, ein Metallstab in zwei Hälften geteilt und in der Mitte mit einem Signal bespeist. Der Name geht auf den deutschen Physiker Heinrich Hertz zurück, der als Erster elektromagnetische Wellen im Experiment nachwies.

Der russische Physiker Alexander Stepanowitsch Popow empfing 1895 dann erstmals elektromagnetische Wellen mit der Dipolantenne. Eine solche Antenne kombiniert die Induktivität des Metallstabes mit der Kapazität zwischen den Stabenden und funktioniert somit als Schwingkreis.

Wird dieser Schwingkreis in Resonanz betrieben, fließen auch bei kleinen Eingangssignalen große Ströme. Diese wiederum erzeugen entsprechend starke elektromagnetische Felder, die sich im freien Raum mit Lichtgeschwindigkeit ausbreiten.

Die Antenne wird auf die Resonanzfrequenz abgestimmt

Die Resonanz lässt sich auch als stehende Welle auf dem Dipol betrachten, wobei der Dipol eine halbe Wellenlänge lang ist. Im Umkehrschluss bedeutet dies, dass die geometrische Dimension der Antenne auf die gewünschten Resonanzfrequenzen abzustimmen ist.

Anders ausgedrückt muss ein gut angepasster Übergang einer Eingangsimpedanz von 50 Ω auf den Wellenwiderstand des freien Raumes (377 Ω) realisiert werden. Dazu und auf Grund unzähliger neuer Anwendungen entwickeln Ingenieure immer neue Antennen, welche auf der Dipolantenne aufbauen. Daraus ergeben sich bisher folgende Anwendungen:

• Antennen werden mehr und mehr integriert und daher miniaturisiert. Sie werden auf Leiterplatten gedruckt oder in Gehäuse von Geräten integriert. Die Miniaturisierung führt dazu, dass die Dimensionen einer Antenne wesentlich kleiner als eine halbe Wellenlänge sind. Außerdem sind bei der Integration Wechselwirkungen mit der restlichen Elektronik zu vermeiden.

• Je nach Anwendung müssen Antennen an ein breites Frequenzband oder ein oder mehrere schmalere Frequenzbänder angepasst werden. Die Anpassung auf mehrere Frequenzbänder ist auch im Zusammenhang der Integration mehrerer Wireless-Funktionalitäten (drahtlose Kommunikation) in sogenannten mobile Devices (tragbaren Geräten) wichtig.

• Außerdem sind die Anforderungen an die Richtcharakteristik einer Antenne entsprechend der jeweiligen Anwendung sehr unterschiedlich. Für mobile Devices sollte die Abstrahlung gleichmäßig in alle Richtungen gehen, wogegen ein Mobilfunk-Sendemast möglichst nur einen Sektor, diesen aber gleichmäßig abdecken sollte. In der Satellitenkommunikation ist die Richtcharakteristik besonders ausgeprägt, da die Signale über sehr weite Distanzen gesendet werden müssen.

Um diesen vielfältigen Anforderungen gerecht zu werden, wurden sehr verschiedene Antennenformen entwickelt: Patch-Antennen, Schlitz-Antennen, welche ein wenig an Lochbleche erinnern, Apertur-Strahler sind meist an weiß-roten Masten hoch oben angebracht, Antennen-Arrays, Vivaldi-Antennen erinnern durch ihre Form an einen Vogelschnabel oder Pacman, und viele andere.

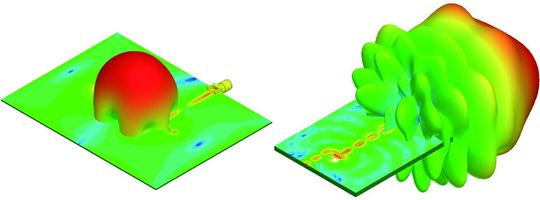
Leistungsfähige Feldlöser ermöglichen die Simulation

Das Programm basiert auf mehreren leistungsfähigen Feldlösern, die sowohl den Frequenz- als auch den Zeitbereich abdecken. Die numerische Herangehensweise basiert auf einem unstrukturierten Netz, um beliebige Geometrien gut abbilden zu können. Der Finite-Elemente-Löser arbeitet im Frequenzbereich und löst die Wellengleichung auf einem Tetraedernetz. In jedem Tetraeder wird das elektrische Feld durch einfache polynomiale Ansatzfunktionen dargestellt, die mit der Bildung der Rotation konform sind. Dies führt zu endlich vielen Freiheitsgraden und einer Diskretisierung des Vektor-Laplace-Operators (Doppelrotation).

Da der Laplace-Operator lokal ist, führt dies zu einem dünn besetzten, linearen Gleichungssystem für das elektrische Feld, welches effizient gelöst werden kann. Die Genauigkeit einer Feldlösung mit Hilfe finiter Elemente hängt von der Netzdichte ab. Dies ist darauf zurück zu führen, dass die Interpolation der elektrischen Felder durch einfache Ansatzfunktionen errechnet werden.

(ID:43100648)