Anbieter zum Thema
Die Auswirkung von Intermodulationsverzerrungen
Das nachfolgende Beispiel zeigt die Auswirkung von Intermodulationsverzerrungen auf die Modulationsqualität (EVM). Bei einem OFDM-Signal (OFDM = Orthogonal Frequency Division Multiplexing) sind alle Träger in einem Abstand von Δf zueinander angeordnet. Die von jedem Trägerpaar erzeugten Intermodulationsprodukte dritter Ordnung fallen genau mit Trägern links und rechts des Trägerpaars zusammen. Die Signalqualität in einem OFDM-System wird daher in erheblichem Maß von Intermodulationsverzerrungen beeinflusst.
Auf zwei Träger mit QPSK-Modulation folgen jeweils zwei ungenutzte Träger. Die Intermodulationsprodukte fallen jeweils bei den Frequenzen der ungenutzten Träger links und rechts des modulierten Trägerpaars an. Analysiert man die Konstellationsdiagramme der ungenutzten Träger, so lässt sich die Signalverzerrung aufgrund von Intermodulationsprodukten bestimmen. Die Phasenlage der Intermodulationsprodukte zueinander – die für ein konstruktives oder destruktives Intermodulationsverhalten bestimmend ist – ist leicht erkennbar.
Die erwarteten Konstellationspunkte der ungenutzten Träger liegen im Ursprung des Konstellationsdiagramms. Aufgrund von Intermodulationsverzerrungen verlagern sich diese Punkte vom Ursprung weg. In einem realen OFDM-System würden diese Träger natürlich nicht analysiert. Für Demonstrationszwecke jedoch veranschaulicht dieser Ansatz den Einfluss von Intermodulationsauslöschung auf den gemessenen EVM-Wert.
In der nächsten Anordnung ist das Messobjekt in den Signalpfad geschaltet (Signalpfad 2 in Bild 3), und die Eingangsdämpfung beträgt 5 dB. Bei dieser Eingangsdämpfung trägt der Spektrumanalysator nicht zur Intermodulationsverzerrung bei, d.h. das Ergebnis wird nur durch die Intermodulationsprodukte des Messobjekts beeinflusst. Schließlich wird die Eingangsdämpfung auf 0 dB reduziert, und die Intermodulationsprodukte des Messobjekts und des Spektrumanalysators interagieren miteinander. Aufgrund der Tatsache, dass die Intermodulationsprodukte gegenphasig sind, kommt es zu destruktiver Interferenz, die Intermodulationsprodukte löschen sich gegenseitig aus. Die Symbole im Konstellationsdiagramm rücken wieder näher an den idealen Punkt (Referenzsymbol) im Ursprung des Diagramms, mit der Konsequenz eines deutlich niedrigeren EVM-Werts. Das heißt, die gemessene Modulationsqualität des Messobjekts ist erheblich besser als der tatsächliche Wert.
Wie die Intermodulationsverzerrung abgeschätzt wird
Eine Auslöschung oder Verstärkung von Intermodulationsprodukten ist unvermeidlich, wenn Messobjekt und Spektrumanalysator einen ähnlich hohen TOI aufweisen. Der wahre Wert der Amplitude PΔ des Messobjekts wird durch die Intermodulationsprodukte des Spektrumanalysators verzerrt. Es ist die Aufgabe des Anwenders, die erforderliche Eingangsdämpfung zu bestimmen, um den durch die Intermodulationsprodukte des Spektrumanalysators verursachten Fehler auf ein akzeptables Maß zu reduzieren.
In den vorangegangenen Beispielen beträgt der gemessene TOI des des Gerätes R&S FSQ26 15 dBm und der des Messobjekts 10 dBm.
Mit der zweiten Gleichung lassen sich die Amplituden PΔ der Intermodulationsprodukte berechnen. Bei einer Eingangsamplitude am ersten Mischer von -10 dBm beispielsweise generiert der R&S FSQ26 Intermodulationsprodukte mit PΔ,SA = 50 dB (TOI = 15 dBm) und das Messobjekt mit PΔ,DUT = 40 dB (TOI = 10 dBm). Liegen die Amplituden der Intermodulationsprodukte des Spektrumanalysators nur 10 dB unter denen des Messobjekts, so führt das bereits zu deutlicher Interferenz – konstruktiv oder destruktiv – je nach Phasenlage der Intermodulationsprodukte zueinander. Bei Interferenz zwischen den Intermodulationsprodukten von Spektrumanalysator und Messobjekt ergibt sich der resultierende Amplitudenfehler eA wie folgt:
Dabei ist d die negative Amplitudendifferenz zwischen den Intermodulationsprodukten des Spektrumanalysators und des Messobjekts in dB (im obigen Beispiel -10 dB). Bei gleichphasigen Intermodulationsprodukten addieren sich die Elemente in der Klammer der Gleichung. Bei gegenphasigen Produkten findet eine Subtraktion statt. Unter der Annahme, dass die Intermodulationsprodukte gegenphasig sind und sich somit gegenseitig auslöschen, errechnet sich der Amplitudenfehler für das obige Beispiel wie folgt:
Das bedeutet, dass die gemessene Amplitude der Intermodulationsprodukte des Messobjekts um 3,3 dB unter dem tatsächlichen Wert liegt.
Wenn sich die Intermodulationsprodukte auslöschen
Um Interferenzen zu vermeiden, muss der Eingangspegel am ersten Mischer des Spektrumanalysators reduziert werden. Dazu wird die Eingangsdämpfung erhöht. Wird die Eingangsdämpfung in obigem Beispiel um 10 dB, so verringert sich der Eingangspegel Pin um 10 dB erhöht auf -20 dBm, und man erhält PΔ,SA = 70 dB. Der Wert PΔ, DUT bleibt bei 40 dB. Nun liegen die Amplituden der Intermodulationsprodukte des Spektrumanalysators um 30 dB unter den Amplituden des Messobjekts. Der resultierende Amplitudenfehler verringert sich auf:
Sind die Amplituden der Intermodulationsprodukte von Messobjekt und Spektrumanalysator gleich groß, also wenn d = 0 dB ist, so kommt es zu einer vollständigen Auslöschung der Intermodulationsprodukte, und der Amplitudenfehler, der in dB gemessen wird, nimmt einen unendlichen Wert an.
Es erscheint an dieser Stelle sinnvoll, zunächst den maximal zulässigen Amplitudenfehler eA für die jeweilige Anwendung zu bestimmen.
Dieser kann wie folgt berechnet werden: IM-Verstärkung: 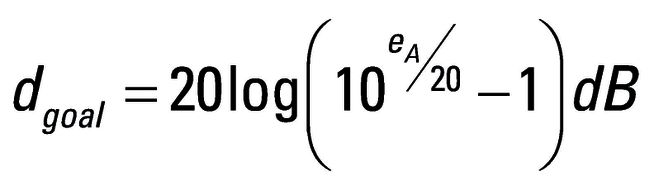
Über die Anfangs dargestellt Gleichung lässt sich PΔ für das Messobjekt und den Spektrumanalysator berechnen. Ist die aktuell gemessene negative Amplitudendifferenz dcurr = PΔ,SA – PΔ,DUT kleiner als die Solldifferenz dgoal, so muss der Mischereingangspegel reduziert werden, um die Intermodulationsprodukte des Spektrumanalysators zu reduzieren. Der optimale Mischerpegel verschiebt sich demzufolge hin zu einem niedrigeren Wert. Dieser Sachverhalt lässt sich als effektiver TOI ausdrücken, also als ein um dgoal /2 verminderter TOI:
Für das Beispiel mit dgoal = 30 dB, dcurr = 10 dB und TOI = 15 dBm ergibt sich ein effektiver TOI von 0 dBm. Dies würde die Kurven im Dynamikbereichsdiagramm entsprechend verändern. Die Amplitudenfehler-Forderung verschiebt die Kurve für die Intermodulationsprodukte dritter Ordnung um dgoal nach oben, während der optimale Mischerpegel einen niedrigeren Wert annimmt.
Für diese Pegelanpassung muss jedoch eine Einschränkung des Dynamikbereichs in Kauf genommen werden. Damit kommt auch dem spezifizierten Dynamikbereich eines Spektrumanalysators besondere Bedeutung zu. Analysatoren mit einem höheren spezifizierten Dynamikbereich können eine Reduzierung des Mischereingangspegels besser auffangen.
Die zur Senkung des Mischereingangspegels erforderliche Erhöhung Att der Eingangsdämpfung ergibt sich wie folgt:
Im obigen Beispiel sind das also 10 dB.
Literatur
[1] Grundlagen der Spektrumanalyse. C. Rauscher, Rohde & Schwarz, 2001
* Dr. Michael Simon ist Applikationsingenieur bei Rohde & Schwarz in München.
(ID:42540100)





:quality(80)/p7i.vogel.de/wcms/f4/ca/f4ca5350a448ca833cd05e87703019d6/0128902853v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/ea/2a/ea2a033222605e608a8121bf90cb04c8/0128893388v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/89/6d/896df53a45806826443c1d4b7b954992/0128555431v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/7d/bb/7dbb06378b5a3d4cf0a96a9ea38a0261/0128880826v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/df/09/df09d635cf5ff7dbdd503a559274dadc/0128886473v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/9d/55/9d551aa422d51c415628a615dfad47b1/0128886693v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/38/10/3810d163ae77015a84eb8d9e0ccdb3f2/0128871470v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/d8/80/d880f26a5e6b9488861f1d713f085023/0128847366v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/00/cf/00cfd71f9b1e00f7d572558ae654362e/0128838981v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/d6/cf/d6cf6e7d535319f6c7b80c0196c06780/0128790900v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/46/95/4695fb8b40fad52300436b044da4ea67/0128770184v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/6e/67/6e67b8257b53970fc9bac7f09d9f5afe/0128880777v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/48/30/48309116c311427f0604cda4fcb92b26/0128891078v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/7f/a6/7fa68cc7dbda0e40809e6ec2a064d3a9/0128830887v3.jpeg)
:quality(80)/p7i.vogel.de/wcms/9c/35/9c35ed04fa562b190cbc496a695a6802/0128823288v1.jpeg)
:quality(80)/p7i.vogel.de/wcms/d7/e6/d7e6fe4124ec2efc726e9c3f2c2a4cfc/0128241940v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/7d/68/7d68aecf780e15057f14df63731fb935/0127934402v3.jpeg)
:quality(80)/p7i.vogel.de/wcms/ec/ad/ecad1a990fb931892757865d0270eabb/0127959299v1.jpeg)
:quality(80)/p7i.vogel.de/wcms/d0/31/d0318b5503cd12a34eef53941547fff8/0128912090v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/d4/ff/d4ffb5ae3f9a2d9755b395cfe082d391/0128875656v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/52/bb/52bbdf63addc5652d9fc2f8908124327/0128808573v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/65/a2/65a2ec3da11379e70bf8933d1170353c/0128776801v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/c7/2f/c72f9de0f70aa2e496a4001d4267032a/0128804348v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/32/93/3293abe43d16822fba0c2f7b16ebf84e/0128782553v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/45/fe/45feae490305c591ce1428c2e13cc34c/0128897569v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/2a/2c/2a2c4d29a353c1aa8abc39c5ddf6c96b/0128894213v3.jpeg)
:quality(80)/p7i.vogel.de/wcms/ee/0f/ee0f3ba5bbfdcf51a749a3844f59320c/0128870257v3.jpeg)
:quality(80)/p7i.vogel.de/wcms/d9/6d/d96dfa3d82837cca1dc111b292abba9a/0128893036v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/64/63/6463f6d5382f7deb935d82c0a23acbfe/0128885787v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/69/1f/691f39ba12be3cad90eb88bdabc456a6/0127321404v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/6a/cc/6acc4f803241cfe5b6d60560c0a2b4d9/0126684948v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/ef/aa/efaae5a25fb0a4c55c434611033447af/0126532350v2.jpeg)
:fill(fff,0)/p7i.vogel.de/companies/64/21/64219ce08bf52/logo.jpeg)
:fill(fff,0)/p7i.vogel.de/companies/68/a4/68a47beec75ce/logo-cmyk-de.jpeg)
:fill(fff,0)/images.vogel.de/vogelonline/companyimg/68800/68851/65.jpg)
:quality(80)/images.vogel.de/vogelonline/bdb/697700/697763/original.jpg)
:quality(80)/images.vogel.de/vogelonline/bdb/697700/697764/original.jpg)
:quality(80)/images.vogel.de/vogelonline/bdb/697700/697765/original.jpg)
:quality(80)/images.vogel.de/vogelonline/bdb/697700/697766/original.jpg)
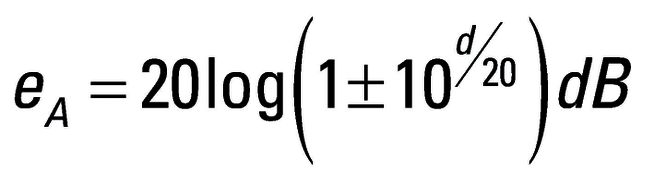
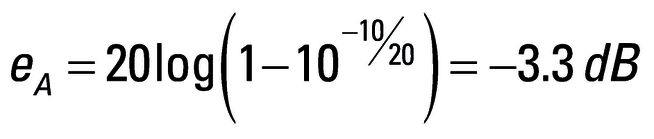
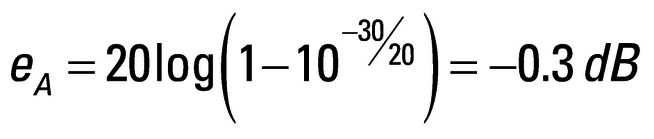
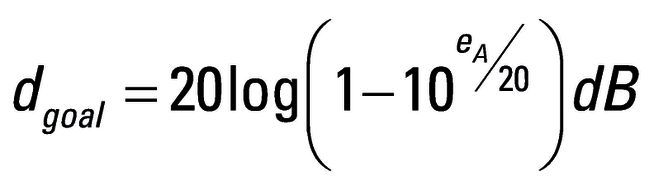
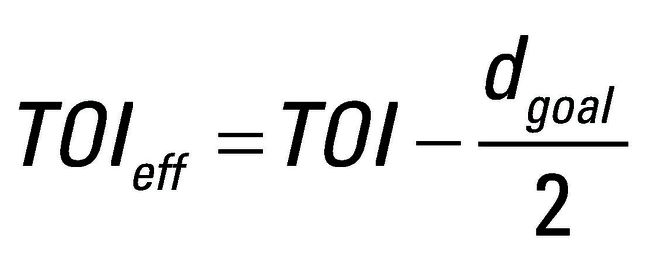
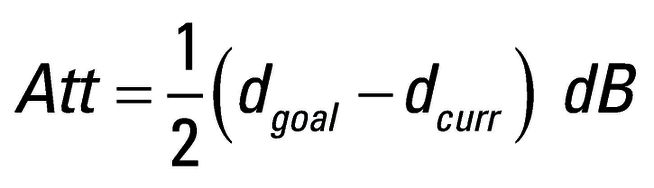
:quality(80)/p7i.vogel.de/wcms/13/38/1338abf2c04d788827c237de1f492187/0125175369v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/3e/4e/3e4e43965e088cc45fe85e4b8eea61ea/0124991114v2.jpeg)