Warum Power-Systeme für schnelle, digitale ICs korrekt ausgelegt sein müssen

Anbieter zum Thema

Würth Elektronik eiSos GmbH & Co. KG

Precoplat Präzisions-Leiterplatten-Technik GmbH

Keysight Technologies Deutschland GmbH

DCC Dirks Compliance Consulting

Die „Stützfähigkeit“ des Kondensators lässt sich an drei Fragen bewerten

Die „Stützfähigkeit“ des Kondensators lässt sich im Wesentlichen an drei Fragestellungen festmachen:

• 1. Wie niederohmig der Kondensator bestenfalls wird?
• 2. Wie lange es dauert, bis er niederohmig ist?
• 3. Wie lange er niederohmig bleibt?

Die Antwort auf die erste Frage, ergibt sich durch Bestimmung des Minimums von Z0C(t) (grüne Kurve). Setzt man Z0C’(t)=0, erhält man t=2L/R. Damit ergibt sich

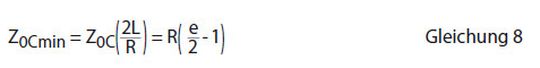
In diesem Beispiel also ein Wert von ca. 100mΩ, was bereits einem Spannungsabfall von rd. 25% entspricht!

Fast noch interessanter ist Frage Nummer zwei: Wie soeben gezeigt, wird das Impedanzminimum erst nach t=2L/R (Zeitkonstante) erreicht. In diesem Beispiel also erst nach gut 14ns!

Im Betrieb eines realen Treibers hätte dies beispielsweise zur Folge, dass es zu einer deutlichen zusätzlichen Verzögerung zwischen triggernder Flanke und Flanke am Ausgang kommt. Denn selbstverständlich können die Ausgangslasten (=Leitungen/Gattereingänge) nur umgeladen werden, wenn entsprechend Strom aus der Versorgung verfügbar ist!

Die dritte Fragestellung wurde bereits beim Betrachten der idealen Kapazität beantwortet: Für t>>2L/R wird das Verhalten der Quellimpedanz bei gegebener Last R nur durch die Kapazität bestimmt. Durch die Wahl ausreichend großer Kapazitätswerte ließen sich folglich auch sehr lang andauernde Strompulse stützen. Eine schöne Lösung – nur leider für das falsche Problem!

Da sich die Dauer der Strompulse an der Flankenzeit der Halbleiter orientiert, werden die Pulse immer kürzer und – dank stetig sinkender Versorgungsspannungen – immer kräftiger. Beide Trends vergrößern das dI/dt, und damit alle Probleme, die durch induktive Anteile bedingt sind, also die Punkte 1. und 2.!

Konstellation hochohmigere Lasten - der Kriechfall

Bei hochohmigeren Lasten (und gleichem L und C) ergibt sich der sogenannte Kriechfall. Die formelmäßige Beschreibung dieser Konstellation ist etwas aufwändiger, da das charakteristische Polynom zwei (verschiedene) Wurzeln hat. Da das Vorgehen aber grundsätzlich dasselbe ist, wird hier auf die Herleitung verzichtet.

Zu den drei vorgenannten Fragestellungen lässt sich für den in Bild 5 gezeigten Kriechfall (Last R=10Ω) folgendes feststellen:

1. Das Impedanzminimum weist einen Wert von ZC0(t)=15mΩ auf.

2. Das Minimum wird bei etwa 1,7ns erreicht.

3. Dank der geringeren Entladung nimmt die Impedanz langsamer zu.

Für eine Dauer von etwa 4ns (von t=1,2ns bis t=5,2ns) bleibt die Quellimpedanz unter dem in unserem anfänglichen Beispiel genannten Zielwert von 50mΩ, was für den betrachteten Strompuls von 1ns Dauer schon sehr großzügig ausgelegt wäre. Doch selbst in dieser relativ harmlosen Konstellation (Last R=10 Ω) dauert es etwas mehr als 1ns, bis die 50-mΩ-Schwelle unterschritten wird.

In der Realität sehen die Verhältnisse geringfügig anders aus, da der Schaltvorgang nicht unendlich schnell vonstatten geht (Schaltzeit der Halbleiter). Der Spannungseinbruch fällt dadurch weniger tief aus, dauert dafür aber auch länger an. Um ein Unterschreiten der 5%-Schwelle (=60mV) zu verhindern wäre in unserem Beispiel eine Flankenzeit von wenigstens 4ns erforderlich. Keine realistische Option angesichts aktueller Flankengeschwindigkeiten im Bereich einiger 100ps.

(ID:331958)