Warum Power-Systeme für schnelle, digitale ICs korrekt ausgelegt sein müssen

Anbieter zum Thema

Würth Elektronik eiSos GmbH & Co. KG

Precoplat Präzisions-Leiterplatten-Technik GmbH

Keysight Technologies Deutschland GmbH

DCC Dirks Compliance Consulting

Ziel: Schnelle Strimpulse stützen

Traditionell nähert man sich diesem Ziel durch den Einsatz von Kondensatoren, frei nach dem Motto „Viel Ladung vor Ort“. Oder etwas technischer ausgedrückt: Betrachtet man den Strompuls im Zeitbereich, entspricht die Fläche unter dem Puls der Ladung, die während der Pulsdauer bereitgestellt werden muss.

Mit Hilfe der Formel

lässt sich ermitteln, wie groß diejenige Kapazität sein muss, aus der sich die Ladung ΔQ entnehmen lässt, ohne dass die Spannung um mehr als ΔU einbricht. Ein Beispiel mag dies veranschaulichen: Sei bei einer Versorgungsspannung von 1,2V ein Einbruch von 5%, also 60mV noch akzeptabel, und sei weiterhin ein Strompuls mit einer Dauer von 1ns auf einer Lastimpedanz von 1Ω zu stützen.

In diesem Fall ergibt sich eine erforderliche Kapazität von 20nF. Rechnet man dieses Beispiel auf ein System hoch, dass eine DC-Stromaufnahme von 10A aufweist, ergibt sich eine erforderliche Kapazität von 167nF. Angesichts der in solchen Systemen durchaus üblichen „Kondensatorgräber“ kommt einem dieser Wert doch ungewöhnlich klein vor! Des Rätsels Lösung ist die Tatsache, dass es sich bei Kondensatoren, anders als bei dem Rechenbeispiel, nicht um reine Kapazitäten handelt! Nachfolgende Überlegungen sollen verdeutlichen, weshalb reale Kondensatoren „ziemlich miese“ Kapazitäten sind.

Berechnung des Zeitverhaltens von Stützkondensatoren

Ein theoretisches Stützungs-Szenario könnte wie folgt aussehen: Der Stützkondensator ist auf U0 aufgeladen, Kondensator und Last (z.B. ein IC) sind impedanzfrei miteinander und über Leiterbahnen mit dem Spannungsregler verbunden. (In der Praxis nicht realisierbare Vereinfachung.)

Zum Zeitpunkt t=0 wird der IC bezüglich seiner Vcc-/GND-Pins niederohmig (z.B. Lastimpedanz=1Ω), um nach 1ns wieder in einen hochohmigen Zustand zurück zu kehren. Würde es sich um eine reine Kapazität handeln, würde sofort Strom fließen. Da die Spannung auf dem Kondensator nicht springen kann, würde bei t=0 noch die volle Spannung U0 auf dem Kondensator stehen – optimale Stützung also!

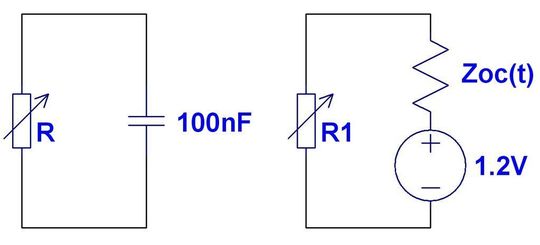
Da sich die Qualität der Stützung an diesen zwei Größen bemisst, wäre es handlich, diese in einem anschaulichen Maß zusammen zu fassen. Zu diesem Zweck führen wir ein (etwas unkonventionelles) Ersatzschaltbild für die Kapazität ein: Wir betrachten die Kapazität als ideale Spannungsquelle mit Quellimpedanz Z0C wie in Bild 1 rechts dargestellt. Dieses Ersatzschaltbild hat natürlich nichts mit den physikalischen „Innereien“ eines Kondensators zu tun, sondern es soll lediglich bezüglich der angeschlossenen Last dasselbe Verhalten wie die 100-nF-Kapazität in Bild 1 links aufweisen!

Da bei t=0 Strom fließt und gleichzeitig die volle U0=1,2V auf der Last steht, muss die Quellimpedanz zunächst 0Ω betragen!

Sobald nun Strom fließt, sinkt die Spannung am Kondensator gemäß

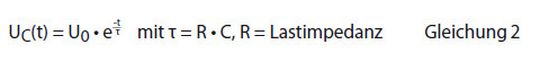
(Zur Vereinfachung wird ein Nachladen des Kondensators während des Strompulses vernachlässigt.)

Zu späteren Zeitpunkten t>0 beobachten wir an den Kondensatorklemmen also eine Spannung, die um ΔU(t)=U0-UC(t) gesunken ist.

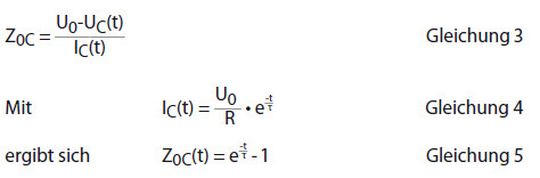
Das soeben eingeführte Ersatzschaltbild erfordert somit eine zeitabhängige Quellimpedanz, auf der die Spannung ΔU(t) „abfällt“:

In Bild 2 ist dieser Zusammenhang zwischen Quellimpedanz und Zeit grafisch dargestellt. Für diesen speziellen Fall wurde angenommen, dass eine 1-nF-Stützkapazität eine 1-Ω-Last stützt.

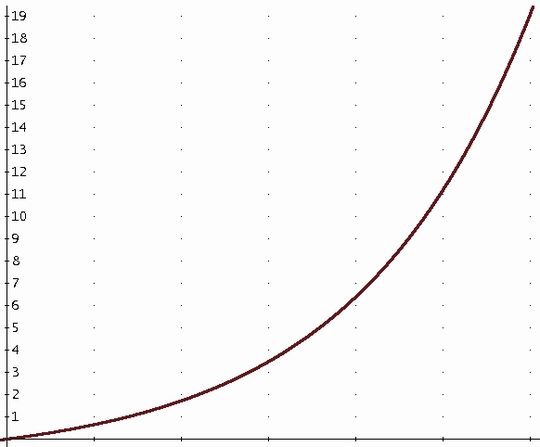
(Zur Vereinfachung wurde von einer konstanten, ohmschen Last ausgegangen). Soll hierbei das eingangs erwähnte 5%-Kriterium erfüllt werden, dürfte die Generatorimpedanz Z0C(t) nicht größer als 50mΩ sein. Diese Bedingung wäre hier für die ersten 50ps erfüllt. Nach 690ps beträgt die Quellimpedanz bereits 1Ω.

Da der „Spannungsabfall“ für eine gegebene Last nur von der Kapazität abhängt, ließe sich dieses Problem relativ leicht lösen: Bei einer 100-nF-Kapazität bliebe die Quellimpedanz bereits für 4,9ns unter 50mΩ! Für den 1-ns-Strompuls aus obigem Beispiel wäre das folglich schon großzügig „überdesignt“.

(ID:331958)