Embedded Computing Warum die klaren Domänen für Soft- und Hardware verschwimmen

Embedded-Computing-Entwickler stehen oft vor einem Dilemma: Schnelle serielle Protokolle lassen sich nicht in Software per Bit-Banging nachbilden. Und eine Hardware eignet sich nicht für die rekursive Suche nach einer Lösung in einer Baumstruktur. Oder vielleicht doch?

Anbieter zum Thema

ISH Ingenieursozietät GmbH

Syslogic GmbH

Eurocircuits GmbH

Arrow Central Europe GmbH

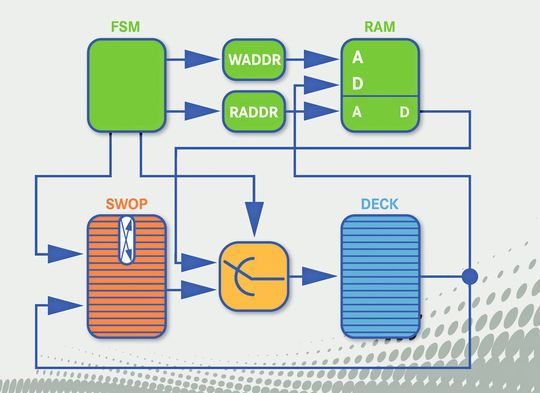
Bei der Entwicklung eingebetteter Systeme muss immer wieder aufs Neue entschieden werden, welche Aufgaben mit Software und welche mit Hardware gelöst werden.

Mikrocontroller als Basis für Software und FPGAs als Basis für Hardware sind heute leistungsfähig und mit einer Unmenge an Funktionen ausgestattet.

Diese geben den Systemarchitekten viel Freiraum bei der Partitionierung.

Beim Distributor Arrow stellt man sich daher die Frage: Gibt es noch klare Domänen für Software und Hardware?

Ein Kartenspiel für den Test Hardware-FPGA contra Software

Im November 2010 hat Al Zimmerman einen Programmierwettbewerb im Internet ausgeschrieben.

Die Aufgabe war, Lösungen für ein fiktives Kartenspiel namens Topswops zu berechnen. Das Spiel hat der Mathematikprofessor John Conway vor fast 40 Jahren erfunden.

Die Spielregeln: Das Kartenspiel hat n Karten. Auf jeder Karte steht eine Zahl von 1 bis n. Jede Zahl kommt genau einmal vor. Die Karten werden gemischt und mit der Zahlenseite nach oben auf einen Stapel gelegt.

Nun beginnt das Spiel: Vom Stapel werden so viele Karten abgehoben, wie die Zahl der obersten Karte anzeigt. Dann dreht man die Reihenfolge dieser abgehobenen Karten um und legt sie zurück auf den Stapel. Das war dann ein Zug, ein Topswop. Das Spiel dauert so lange, bis die 1 oben liegt. Denn einen Teilstapel mit einer Karte umzudrehen, das geht ja nicht.

Die Aufgabe besteht nun darin, die Karten zu Beginn des Spiels so zu mischen, dass die Anzahl von Zügen maximal groß wird.

Eine rechnerische Lösung für das Problem ist bislang nicht gefunden, also bleibt nur, es mit purer Rechengewalt zu versuchen. Interessanterweise enden die meisten Lösungen mit einem Stapel, bei dem die Karten von 1 bis n von oben nach unten durchsortiert sind.

1. Lösungsansatz: Erzeugen von Permutationen

Neben einigen Näherungslösungen gibt es zwei vollständige Ansätze zur Lösung des Spiels:

Zunächst werden in einer großen Schleife alle möglichen Anfangspermutationen erzeugt und das Spiel gemäß den Regeln gespielt. Dieser Ansatz führt aber bereits bei kleinen n zu Rechenzeiten im Stundenbereich, denn die Anzahl von durchzurechnenden Stapeln ist n!.

Selbst wenn man pro Sekunde 1 Milliarde Stapel durchrechnen könnte, was illusorisch ist, würde die Zeit vom Urknall bis heute nicht reichen, um das Spiel mit 28 Karten zu lösen. Und Al Zimmermann wollte Spiele mit bis zu 97 Karten gelöst haben.

2. Lösungsansatz: Rückwärts spielen

Im zweiten Lösungsansatz wird das Spiel rückwärts gepielt. Ausgangspunkt ist der sortierte Stapel. Gesucht werden nun die Zustände, die zu diesem sortierten Stapel geführt haben können. Sind diese gefunden, richtet sich die Suche auf die zuletzt gefundenen Zustände, usw.

Dieser Ansatz funktioniert nicht bei allen Kartenspielen. Denn er setzt voraus, dass man einen Zug rückwärts spielen kann; dass man also ermitteln kann, welche Zustände zu dem aktuellen Zustand geführt haben können.

Beim Kartenspiel Topswops ist das der Fall. Wird vorwärts gespielt, dann landet nach einem Topswop die oberste Karte an der Position im Stapel, die ihrer aufgedruckten Zahl entspricht. Rückwärts gespielt heißt das, dass jede Karte, die an der Position liegt, die ihrer Zahl entspricht, ein Kandidat für einen Rückwärts-Swop ist.

Diese Suche lässt sich programmtechnisch elegant mit einer Rekursion lösen, und so ist ein C Programm, das ein Spiel rückwärts durchrechnet, keine 200 Zeilen lang.

Entwurf einer rekursiven Hardware

(ID:28152470)