Auswahl und Design von Filtern Integrierte Lösungen für passive Interface-Filter- und lineare Aktivfilterdesigns

Ohne Filter ginge in elektronischen Systemen so gut wie nichts. Dabei kann es sich um passive, aktive oder digitale Filter handeln. Entwickler haben deshalb beim Systemdesign die Qual der Wahl, welche Filterlösung in der jeweiligen Anwendung die optimale ist. Kompetente Unterstützung bieten im Zweifelsfall die Supportspezialisten bei Farnell.

Anbieter zum Thema

ET System electronic GmbH

MES Electronic Connect GmbH & Co. KG

DMB Technics AG

Farnell GmbH

Gewöhnlich hat ein Entwickler schon von Anfang an ein bestimmtes Filterverfahren sowie entsprechende Filterarten im Sinn. Zur einfachen passiven Filterung kann eine Trennung der Versorgungsspannungen ausreichen. Bei komplexeren Filteranforderungen sind jedoch mehrere Faktoren zu berücksichtigen. Durch eine etwas umfangreichere Planung zu Beginn eines Projekts lassen sich unter Berücksichtigung verschiedener integrierter Lösungen Kosten und Entwicklungszeit reduzieren und eine Leistungserhöhung erzielen.

Ab der Spezifikationsphase sollten Entwickler eine gute Vorstellung vom erforderlichen Frequenzgang einzelner Filter sowie vom Amplituden- und Frequenzverlauf haben und ungefähr wissen, ob es sich bei den entsprechenden Filtern um Tief-/Hochpass-, Bandpass- oder Kerbfilter-Ausführungen handeln soll. Der Filter muss unter Umständen darauf beschränkt werden, über existierende Versorgungsspannungen zu laufen. Dies ist insbesondere dann von größerer Bedeutung, wenn das System beispielsweise über Niederspannungsbatterien in einem tragbaren Gerät wie zum Beispiel einem MP3-Player betrieben wird. Nach Festlegung der Versorgungsspannungen, Frequenzarten und Frequenzgänge müssen die gewünschten Merkmale der Frequenzgangkurven Standardkurven gleichgesetzt werden.

Bestimmung der Frequenzgangkurve

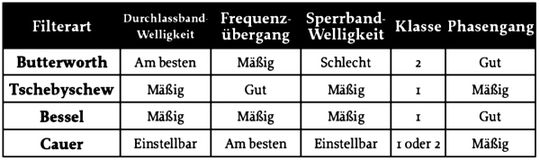
Die Tabelle stellt die gebräuchlichsten herkömmlichen Frequenzgangkurven – Butterworth, Bessel und Tschebyschew – dar. Es existieren viele weitere Frequenzgangkurven, wovon viele auf den obigen Grundkurven basieren und eine höhere Ordnung aufweisen. So besteht beispielsweise der häufig in High-End-Tonweichen eingesetzte Linkwitz-Riley Filter 2. Ordnung aus zwei Butterworth-Filtern 1. Ordnung.

Butterworth-Filter: Das Butterworth-Filter ist die üblichste Filterart, da diese Filter das mathematisch flachste Durchlassband aller Filter aufweisen. Butterworth-Filter sind Filter der Klasse 2, das bedeutet, dass die Welligkeit auf den Sperrbereich beschränkt ist.

Tschebyschew-Filter: Tschebyschew-Filter sind Filter der Klasse 1 und weisen im Vergleich zu Butterworth-Filtern ein steileres Abknicken bei der Grenzfrequenz auf. Im Durchlassband ist jedoch Welligkeit vorhanden.

Cauer-Filter: Cauer-Filter können zur Klasse 1 oder zur Klasse 2 gehören, da sich die Welligkeit im Durchlass- und Sperrband unabhängig voneinander einstellen lässt. Diese Filter weisen darüber hinaus für festgelegte Welligkeitswerte den steilsten Verstärkungsübergang zwischen dem Sperr- und Durchlassband auf.

Bessel-Filter: Bessel-Filter werden für Systeme ausgewählt, für die ein linearer Phasengang erforderlich ist. Sie weisen eine konstante Gruppenlaufzeit im Durchlassbereich auf. Aus diesem Grunde werden sie häufig für Audioschaltungen eingesetzt, bei denen die Beibehaltung einer entsprechenden Wellenform sehr wichtig ist.

Je höher die Ordnung, desto steiler die Frequenzgradienten

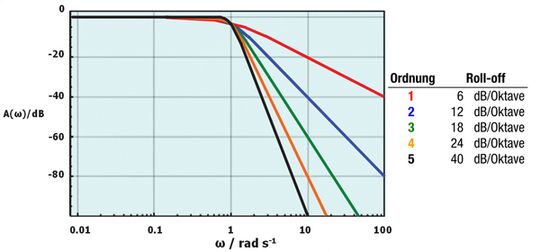
Die „Ordnung“ einer Schaltung wird durch die Anzahl der reaktiven Elemente (induktiv oder kapazitiv) innerhalb der Schaltung bestimmt. Ein einfacher Widerstand und Kondensator zählen beispielsweise als 1. Ordnung, und jede weitere, einer Schaltung hinzugefügte reaktive Komponente erhöht die Ordnung um 1. Jede Ordnung führt bei einer Abstimmung auf dieselbe Frequenz zu einem um jeweils 6dB pro Oktave steiler werdenden Frequenzgradienten. Je höher die Filterordnung, desto steiler fällt der Frequenzgang ab (Bild 1).

Analog oder digital

Ob eine digitale Implementierung angemessen ist, hängt von mehreren Faktoren ab. Eine digitale Implementierung erfordert im Allgemeinen eine längere Entwicklungszeit und mehr Ressourcen und wird nicht unbedingt dieselben Preis-/Leistungsvorteile wie Analogfilter bereitstellen. Bei digitalen Filtern, die Bausteine wie FPGAs oder CPUs umfassen, muss das Analogsignal vor der Filterung zuerst digitalisiert werden, bevor es später wieder in seine ursprüngliche Form umgesetzt wird. DSP-Lösungen bieten eine hochentwickelte Verarbeitungsleistung. Diese zusätzliche Flexibilität bringt jedoch eine längere Entwicklungszeit sowie höhere damit verbundene Kosten mit sich. Eine Entscheidung sollte hauptsächlich basierend auf der Komplexität der anderen in ein Design integrierten Funktionsblöcke erfolgen.

Die unterschiedlichen Vorgehensweisen beim Filterdesign

Die Laplace-Transformation lässt sich über entsprechende Kalkulationen herleiten und wird normalerweise über Gleichungen in Bezug auf Standard-Frequenzgangkurven ermittelt (siehe auch Kasten „Gleichungen“). Zähler und Nenner der Transformation können dann zur Bestimmung der Pole und Nullen der Gleichung faktorisiert werden.

Ein Filter ist stabil, wenn mindestens ebenso viele Pole wie Nullen vorhanden sind

Bei den Polen handelt es sich um die „s“-Werte, die dazu führen, dass der Nenner Null entspricht (oder H(s)=∞), und die „Nullen“ sind die „s“-Werte, die dazu führen, dass der Zähler gleich Null ist. Zur Sicherstellung eines stabilen Filters muss die Anzahl der Pole mindestens der Anzahl an Nullen entsprechen. Da Gleichung 1 aufzeigt, dass nur Pole vorhanden sind, bestätigt dies, dass der Butterworth-Filter 3. Ordnung stabil ist und keine Schwingung vorhanden ist.

Wenn das Zeit-/Amplitudenverhalten eines Filters genauer untersucht werden muss, kann eine umgekehrte Laplace-Transformation an der Gleichung durchgeführt werden, um wieder zur Zeitebene zurückzukehren. Außerdem sollte hier beachtet werden, dass in dem Fall eine Umsetzung zwischen der analogen „s“-Ebene und „z“-Ebene zur digitalen Implementierung möglich ist.

Verschiedene Versionen von Sallen-Key-Aktivfiltern als Tiefpass oder Hochpass

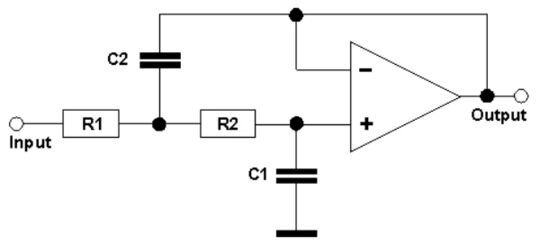
Obwohl für die Endschaltung eine Vielzahl von verschiedenen Konfigurationen basierend auf den jeweiligen mathematischen Beziehungen möglich ist, wurde hier ein zweipoliger Sallen-Key-Filter (2. Ordnung, 12 dB pro Oktave) ausgewählt, da es sich hierbei um die beliebteste Filterkonfiguration 2. Ordnung sowohl für Tief- als auch Hochpassfilteranwendungen handelt. Diese Filter lassen sich einfach konstruieren und sind relativ gut belastbar, was Komponententoleranzen betrifft.

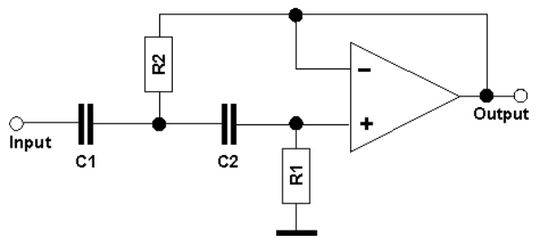
Die Bilder 2 und 3 zeigen Tief- bzw. Hochpass-Versionen. Über eine entsprechende Werteauswahl der Komponenten lässt sich eine beliebige Tiefpassfilterkonfiguration 2. Ordnung erzielen.

Einchip-Lösungen für Analogfilteranwendungen

Wenn Filter hoher Ordnung erforderlich sind, stellen Filter auf Sallen-Key-Basis nicht unbedingt die beste Lösung dar. Unter Verwendung von entsprechenden Schaltkondensator-Filtern, wie beispielsweise Maxims MAX293, sind Filter bis zur 8. Ordnung möglich. Durch Umsetzung der Eingangstaktfrequenz in die gewünschte Roll-on/Roll-off-Frequenz weisen diese Filter eine hohe Flexibilität auf. Gleichzeitig ist jedoch ein höheres Rauschen als bei zeitkontinuierlichen Filtern vorhanden.

Die UAF42-Filter von TI sowie Maxims MAX274-Filter weisen den Vorteil auf, dass sie Tiefpass, Hochpass und Bandpass in einem einzelnen Gehäuse kombinieren. Durch die hochgenau getrimmten internen Kondensatoren sind sie weniger anfällig für Frequenzschwankungen, die zu einem Versatz zwischen den Stufen führen würden.

Für Entwickler, die Filterspezifikationen kurzfristig ändern möchten, eignen sich möglicherweise FPAAs (Field Programmable Analog Arrays / vor Ort modifizierbare Analogbausteine), wie beispielsweise von Anadigm. Diese sind in QFN-Gehäusen mit kleinem Footprint erhältlich und umfassen vollständig konfigurierbare analoge Funktionsblöcke. Der Baustein AN121E04 verfügt beispielsweise über vier konfigurierbare E/A-Zellen und zwei entsprechende Ausgangszellen, wodurch sich mehrere Analogsignale gleichzeitig verarbeiten lassen.

Nach Unterlagen von Farnell Deutschland, Oberhaching

(ID:272177)