Programmierbare Oszilloskope Eigene Funktionen implementieren

Ingenieure, die ihre eigenen Algorithmen in ein Oszilloskop einbinden wollten, konnten das bislang nur Offline erledigen. Nun sind Anwender in der Lage, über definierte Funktionen hinaus ihre ganz speziellen Funktionen in ein Messgerät zu übertragen. Sie brauchen auf kein Firmewareupdate mehr zu warten.

Anbieter zum Thema

TRACO ELECTRONIC GMBH

Precoplat Präzisions-Leiterplatten-Technik GmbH

IBR Leiterplatten GmbH & Co. KG

Teledyne GmbH

Moderne Oszilloskope stellen inzwischen eine breite Vielfalt an Parametermessungen und mathematischen Funktionen bereit. Dennoch war der Umfang der in-Line-Analysefähigkeiten bisher begrenzt. Jetzt besteht die Möglichkeit, externe Algorithmen direkt in die Signalverarbeitung des Oszilloskops zu integrieren. Damit steht die Leistungsfähigkeit mathematischer Software von Drittanbietern zur Verfügung. Anwender können eigene Algorithmen erstellen, um beliebige mathematische Operationen genau so auszuführen. Prüfabläufe lassen sich aus oszilloskopinternen Mathematik- und Messfunktionen zusammengestellen, wobei sich anwenderdefinierte Funktionen problemlos in die Verarbeitung einbeziehen lassen.

Signale und Prüfkriterien werden immer komplexer

Die Entwickler standen bisher immer vor dem Problem, eine festgelegte Anzahl mathematischer Funktionen und Parametermessungen im Oszilloskop zu verwenden. Dazu ruft er Messungen wie Anstiegszeit und Frequenz oder mathematische Funktionen wie Integral und FFT auf. Die Ergebnisse dieser Operationen werden direkt auf der Bedienoberfläche dargestellt. Alle vordefinierten Funktionen sind allgemeine Messanwendungen recht nützlich. Aber die Signale und Prüfkriterien werden immer komplexer. Für solche Anwendungen haben Messtechniker ihre eigenen Algorithmen, die bisher offline ausgeführt werden mussten. Das geschah entweder auf separaten Computern oder auf dem Oszilloskop im Hintergrund, außerhalb der Oszilloskopsoftware. Solche Offlinelösungen können weder unmittelbar ihre Ergebnisse anzeigen, noch ihre Information direkt in der Oszilloskopoberfläche darstellen.

Selbstentwickelte Algorithmen in die Oszilloskopumgebung einbinden

Mit Matlab-in-Line lassen sich anwenderdefinierte Algorithmen direkt in die Oszilloskopumgebung einbinden. Wenn beispielsweise ein Chiphersteller das Ausschwingen nach Pegelwechseln messen will, musste er bisher auf Offlineverarbeitung zurückgreifen, um solch eine komplexe Messung durchzuführen. Nun kann dieser Algorithmus in Matlab erstellt und in die Liste der Oszilloskop-Messfunktionen aufgenommen werden. Auf diese Weise kann vom Oszilloskop die Abklingzeit eines Signals einfach gemessen werden. Vom Oszilloskop werden automatisch statistische Daten dieser Messungen erfasst. Der neue Matlab-Prozess ist jetzt Bestandteil der Fähigkeiten des Oszilloskops. Ein direkter Zugriff auf den Speicher mit den gemessenen Daten ist möglich, und das Oszilloskop kann die Fähigkeiten der Software nutzen, um Messwerte und Ergebnisse mathematischer Funktionen live darzustellen.

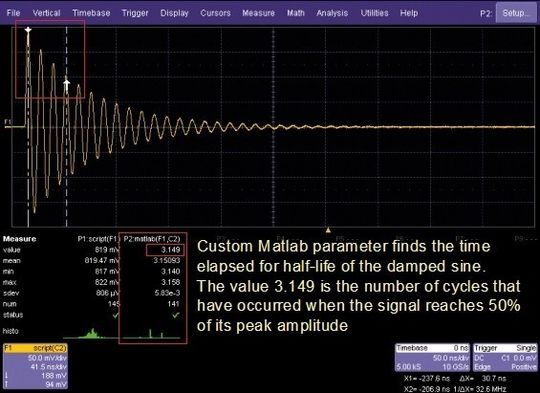
Ein Beispiel soll der zeitliche Abfall einer gedämpften Sinusschwingung geben: Bisher wurden keine Oszilloskope hergestellt, die automatisch den zeitlichen Abfall messen. Wenn ein Matlab-in-Line-Prozess dafür verwendet wird, lässt sich der Abfall durch einen anwenderdefinierten Algorithmus ermitteln und vom Oszilloskop anzeigen. Das erfolgt gemeinsam mit ausgewählten Messergebnissen, wie Anstiegszeit und Pulsbreite. So können beliebige Messungen, die sich in einem Algorithmus beschreiben lassen, direkt als Messwert oder mathematische Funktion darstellen.

Digitale Filterung ist eine der häufigsten mathematischen Anwendungen

Eine der häufigsten mathematischen Anwendungen für Offlineverarbeitung ist die digitale Filterung. Diese Art der Signalkonditionierung kann mit dem Software-Tool einfach vorgenommen werden. Im Offlinebetrieb steht dem Anwender für eine Fehlersuche in Echtzeit keine schnelle Signalanzeige zur Verfügung. Mit der neuen Funktion hat das verarbeitete Signal alle Eigenschaften eines erfassten Signalverlaufs, und die Darstellung wird direkt bei jeder neuen Triggerauslösung aktualisiert. Komplexe Funktionen wie ein Butterworth-Filter 300. Ordnung, die auf einem Oszilloskop so nicht existieren, lassen sich als Funktion einrichten. Sie stehen direkt in der Signaldarstellung des Oszilloskops zur Verfügung. Die Funktion hat alle Eigenschaften eines Standard-Mathematikkanals. Das Ergebnis kann gespeichert, skaliert, mathematisch verarbeitet und insgesamt so verwendet werden, als wäre es ein erfasstes Eingangssignal.

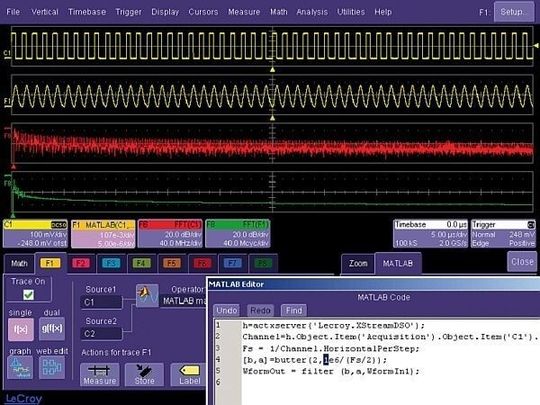
Das Bild zeigt im Matlab-Editor fünf Zeilen Code, der in Funktion F1 ausgeführt wird. Damit wird direkt während der Messung eine Butterworth-Tiefpassfilterung des Eingangssignals von Kanal 1 vorgenommen. Zum Vergleich der Spektraleigenschaften zeigt die rote FFT-Darstellung den Frequenzbereich des Eingangssignals von Kanal 1, während die grüne Darstellung das Signal nach einer In-Line-Tiefpassfilterung von einem MHz.

Frequenzänderungen im Zeitbereich beeinflussen

Eine hilfreiche Funktion ist die spektrale Chirurgie an Signalen. Mit einer inversen FFT-Funktion kann ein Signal aus dem Zeitbereich zunächst per FFT in den Frequenzbereich umgesetzt werden. Jetzt lassen sich Änderungen vornehmen und dann wieder zurück transformieren. Der Anwender erhält eine sofortige Ansicht der Auswirkungen von Frequenzveränderungen eines Signals im Zeitbereich.

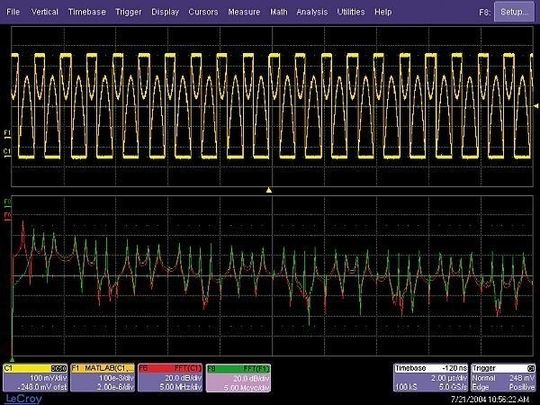
Ein Beispiel dafür zeigt das Bild. Das rechteckförmige Eingangssignal von Kanal 1 wird frequenzverändert und dann mit inverser FFT-Funktion wieder in den Zeitbereich überführt. Die FFTs von Funktion 1 und Kanal 1 zeigen, dass die Grundschwingung komplett unterdrückt werden kann, während die Harmonischen vollständig intakt sind.

Signale ohne Nullanteil (NRZ, Non-Return-to-Zero) verwenden zwei logische Pegel (Low und High) zur Darstellung von logisch Eins und logisch Null. Herkömmliche Oszilloskope können solche Signale erfassen und darstellen. Sie haben aber nicht die Fähigkeit, die Signale in ihre binären digitalen Entsprechungen zu dekodieren. Moderne Oszilloskope können jetzt die Signale nach Anwenderkriterien dekodieren.

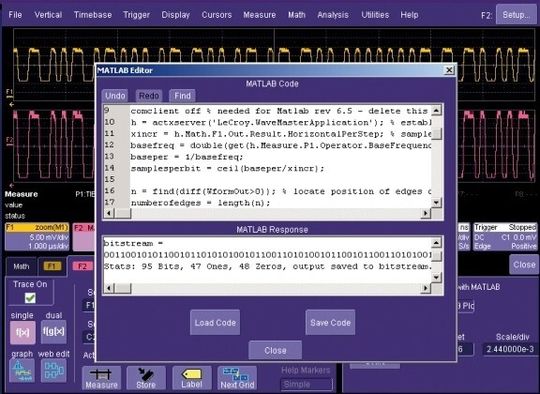
In diesem Bild wurde ein Block von NRZ-Daten als Funktion F1 erfasst. Der Parameter TIE@lv (Zeitintervallfehler bei einem bestimmten Pegel) wird als Parameter P1 angewendet. Die virtuelle Taktfunktion des TIE meldet eine zugrunde liegende Bitrate von 2,488 GBit/s. Das entspricht einem OC-48 Datenstrom. Funktion F2 gestattet durch ein anwenderdefiniertes Script die automatische Dekodierung jedes Signals, wie das zweite Bild zeigt.

Der Algorithmus liest die Grundfrequenz aus dem TIE-Parameter aus, um so die Blockgrenzen zwischen den UIs zu finden. Während der Algorithmus die einzelnen Signalflanken verarbeitet, schreibt er den logischen Wert in einen Datenpuffer. Ist die Schleife durchlaufen, wird das digital dekodierte Signal und seine Statistik angezeigt und in eine Datei gespeichert. Der Vorgang wiederholt sich bei jeder Erfassung, was eine schnelle in-Line Signalumsetzung gestattet. Mit den in logische Werte umgewandelten Daten ließe sich die Funktion bis zur Protokollebene erweitern, indem Sequenzen von Nullen und Einsen mit Hilfe einer Matlab-Referenztabelle bestimmten Bytewerten zugeordnet werden.

Signalinhalte werden in Echtzeit bewertet

Herkömmliche Mathematik- und Messfunktionen liefern numerische Ergebnisse. Mit dem neuen Tool können diese Fähigkeiten um einen neuen Bereich von Messungen und Mathematik erweitert werden, in dem auch Echtzeitbewertungen von Signalinhalten getroffen werden. Die Funktion bietet direkten COM-Objektzugriff auf jede Oszilloskop-Objekteigenschaft. Einstellungen wie Trigger, Zeitbasis oder Kanaleinstellung können direkt und ohne weitere Softwareunterstützung gelesen und implizit verändert werden.

Wenn zum Beispiel das Oszilloskop ein Signal erfasst und dessen Pulsbreite bestimmt, kann es gleichzeitig die Signalamplitude beobachten. So lässt sich feststellen, ob das Signal übersteuert und begrenzt wird. Wenn das so ist, lässt sich die Vertikalablenkung so anpassen, dass das Signal in den vertikalen Aussteuerungsbereich gelegt wird. Diese Art von geschlossener Rückkopplung liefert Messungen, die direkt bestimmte Einstellungen des Oszilloskops beeinflussen können. Das erfolgt über die Gewinnung komplexer mathematischer und messtechnischer Ergebnisse hinaus.

Im Bild ist ein Beispiel dargestellt, wie eine Matlab-Funktion die Lage des Signals in Bezug auf die sechseckige Maske vergleicht. Die entsprechenden COM-Objekte werden überwacht. Dadurch kann das laufende MATLAB-Script die vertikale Ausrichtung des Signals zur Maske kontrollieren und führt diese aktiv nach, um das Signal jederzeit von der Maske entfernt zu halten.

Mathematische Funktionen beliebig erweiterbar

Es gibt eine neue Kategorie von Oszilloskopfunktionen: Anwenderdefinierte Matlab-Funktionen in mathematische Funktionen und Messfunktionen aufnehmen. Die Integration erweitert die mathematischen und messtechnischen Möglichkeiten von herkömmlich vordefinierten Funktionen. Anwender müssen nicht mehr darauf warten, dass ein Oszilloskophersteller genau ihre Funktion in die Firmware einbaut. Die Funktion kann vom Anwender unmittelbar implementiert werden und steht damit sofort zur Verfügung. Messungen, die heute noch gar nicht definiert sind, können zu einem beliebigen Zeitpunkt erstellt und hinzugefügt werden. Sensible, kundenspezifische Messfunktionen müssen nicht mehr einem Messgerätehersteller offengelegt werden. Sobald eine Funktion durch einen Algorithmus beschrieben werden kann, sind die analytischen Fähigkeiten eines Oszilloskops nur noch durch den Ideenreichtum des Anwenders begrenzt.

*Mike Hertz ist Field Application Engineer bei der LeCroy Corp.

(ID:223274)