Anbieter zum Thema
Das Quantisierungsrauschen eines Wandlers
Bei der Digitalisierung zeitlich veränderlicher Eingangsspannungen wirkt sich die Quantisierungsabweichung eines A/D-Wandlers als eine Art Rauschsignal aus, das dem ideal ermittelten Nutzsignal überlagert erscheint. Das mittlere Verhältnis zwischen eigentlichem Nutzsignal und dem Quantisierungsrauschen wird als Signal-Rausch-Verhältnis (SNR) angegeben.
Wie in der Analyse höherfrequenter Signale üblich, verrechnet man nicht Spannungen, sondern Leistungen. Genauer gesagt die mittleren Signalleistungen, die umgesetzt würden, wenn man die Spannungen auf einen ohmschen Widerstand von 50 Ohm wirken ließe. Um verschiedene A/D-Wandler bezüglich ihres SNR zu vergleichen, verwenden die Hersteller der A/D-Wandler-Chips als Nutzsignal ein Sinussignal, das über den gesamten Eingangsspannungsbereich schwingt mit einer Nulllinie genau in der Mitte. Es zeigt sich, dass hierfür folgender Zusammenhang gilt (n Auflösung in Bit, PN = Nutzsignalleistung und PR = Rauschsignalleistung).
Ein A/D-Wandler mit einer mittleren Auflösung von 12 Bit verfügt über ein SNR von ca. 74 dB. Dieser Zusammenhang bezieht sich auf ein Nutzsignal, das den gesamten Eingangsspannungsbereich umfasst. Für kleinere Nutzsignale schrumpft das Verhältnis.
Das Bild 3 zeigt die drei wesentlichen Abweichungen realer A/D-Wandler-Kennlinien von der in Bild 2 als ideal angenommenen. Nullpunkt- und Verstärkungsabweichungen können in einem gewissen Maße durch zwei Kalibriermessungen automatisch innerhalb des Chips oder manuell durch den Anwender reduziert werden. Die Linearitätsabweichung entsteht, in dem die Breite einzelner Stufen von der Idealbreite fertigungstechnisch abweicht. So führt die gezeigte Verbreiterung einer Stufe zu einem Abflachen des weiteren Kennlinienverlaufs.
Möchte man für ein konkretes A/D-Wandler-Exemplar die Linearitätsabweichung für jede Stufe im Detail angeben, so haben sich zwei Fachbegriffe herausgebildet: DNL und INL. Die Differentielle Nichtlinearität DNL (i) gibt für jede Stufe i die positive bzw. negative Abweichung von der Idealbreite an in Einheiten von LSB (Least Significant Bit); 1 LSB entspricht der Idealbreite. Durch Aufsummieren der DNL (i) über alle Stufen bis zur Stufe k erhält man die Integrale Nichtlinearität INL (k).
Da ein A/D-Wandler eine gewisse Umsetzzeit benötigt, um ein analoges Signal in einen digitalen Wert abzubilden, lassen sich zeitlich veränderliche Signale nur in bestimmten minimalen Zeitabständen TA digitalisieren oder abtasten. TA heißt entsprechend auch Abtastzeit. Aufwendigere Hardwareimplementierungen schalten vor den eigentlichen A/D-Wandler ein Sample-and-Hold-Glied. Das ist eine Analogschaltung, die mit einem Triggerimpuls zum gewünschten Abtastzeitpunkt den Spannungswert des Analogsignals für die Dauer der Analog-Digital-Umsetzung speichert.
Für einfachere Hardwareimplementierungen, wie einige sehr kostengünstige USB-Messmodule, die über kein Sample-and-Hold-Glied verfügen, soll abgeschätzt werden, welche zusätzliche Abweichung bei der Digitalisierung entsteht. Ein exemplarisches Sinussignal wird an seiner steilsten Stelle, dem Nulldurchgang, digitalisiert. Während der durch den jeweiligen Typ des A/D-Wandlers bedingten Umsetzzeit TU ändert sich das Signal näherungsweise proportional zu TU und der Steigung des Sinussignals im Nulldurchgang:
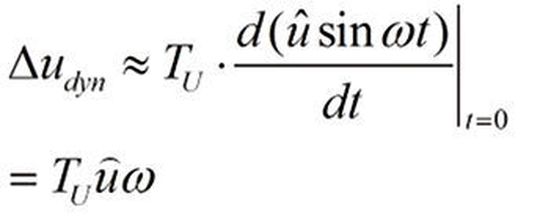
Am Beispiel eines Sinussignal der Frequenz 1 kHz mit einer Amplitude von 1 V an, so ergibt sich bei einer Umsetzzeit von 100 µs – das immerhin nicht mehr als ein Zehntel der Periodendauer des Signals – bereits ein Δudyn von etwa 0,63 V! Es hängt jetzt vom im Chip des A/D-Wandlers verwendeten Umsetzverfahren und der zeitlichen Interpretation des Abtastzeitpunkts in der Auswertesoftware ab, ob sich die Änderung komplett oder teilweise als dynamische Messabweichung zusätzlich auswirkt.
Ein bandbegrenztes Signal muss mit einer Frequenz, die mehr als das Doppelte der maximal im Signal auftretenden Frequenz beträgt, abgetastet werden, damit es theoretisch vollständig rekonstruiert werden kann. Bei einem bandbegrenzten Signal ist im beliebig zeitlichen Verlauf nehmenden Signal keine höhere Signalfrequenz enthalten, als die der Kalkulation zugrunde liegende, was durch entsprechende Filter sichergestellt wird.
Das in der Praxis anzutreffende Missverständnis bezieht sich darauf, dass bei den meisten Anwendungen eine Rekonstruktion des Originalsignals in der Messdaten-Applikation – beispielsweise durch Interpolationsverfahren - gar nicht durchgeführt wird. Sämtliche enthaltenen Verarbeitungs- wie auch Visualisierfunktionen basieren ausschließlich auf den Abtastwerten selbst.
Um sinnvolle Ergebnisse zu erhalten, muss das Signal deutlich höher abgetastet werden, als es nach dem Abtasttheorem notwendig ist. Die dem Originalsignal entsprechende Pixel-genaue Darstellung auf einem Bildschirm rein unter Verwendung der Abtastwerte ergibt hierzu eine gute Abschätzung: Soll beispielsweise bei einer Auflösung von 1920 × 1080 Pixeln (entspricht einer HD-Auflösung) eine Periode eines periodischen Signals über ein Drittel der Bildschirmbreite lückenlos dargestellt werden, so sind 640 Abtastungen pro Periode notwendig. Das ist deutlich mehr als die Untergrenze von zwei Abtastungen gemäß Abtasttheorem.
Quelle
Jörg Böttcher: Kompendium Messdatenerfassung und -auswertung. ISBN 978-3-7386-2255-3 (Paperback) bzw. ISBN 978-3-7392-7714-1 (E-Book), Verlag: Books on Demand.
* Prof. Dr.-Ing. Jörg Böttcher hat eine Professur für Regelungstechnik und Elektrische Messtechnik an der Universität der Bundeswehr in München inne.
(ID:44076972)





:quality(80)/p7i.vogel.de/wcms/c1/94/c19403fe0194686b2f4911be7e1e9539/0129294209v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/e6/72/e67279e23a3267a463edf3e3f55c8e81/0129260553v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/51/96/51962a77f2a4b260373b39a489f53df9/0129137248v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/4b/c5/4bc5a6e591592fac9c3f05b77b8c237f/0129307845v4.jpeg)
:quality(80)/p7i.vogel.de/wcms/6c/22/6c22d187c749f899845158057cb92ad1/0129224894v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/f5/51/f5516128b6a3176679f3291ef1f3c594/0129209328v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/7b/57/7b5725dd2e7545ab4904a9b7a3735721/0129309389v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/b2/9c/b29ce10d1817d4b67968dfb737d812b7/0129308255v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/4c/f0/4cf066b46a5fcfc430a2454a5e82e801/0129279386v1.jpeg)
:quality(80)/p7i.vogel.de/wcms/4e/f2/4ef224fde728985d8b9630eb0fa37909/0129293948v3.jpeg)
:quality(80)/p7i.vogel.de/wcms/3f/0d/3f0d634d8c172031474c341b3a2b725e/0129262158v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/40/32/4032d23b67ab8a52bf472277dc70a64f/0129074969v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/66/0c/660c31afa35398bac9be42f2be73fdc4/0129073529v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/9c/35/9c35ed04fa562b190cbc496a695a6802/0128823288v1.jpeg)
:quality(80)/p7i.vogel.de/wcms/d7/e6/d7e6fe4124ec2efc726e9c3f2c2a4cfc/0128241940v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/7d/68/7d68aecf780e15057f14df63731fb935/0127934402v3.jpeg)
:quality(80)/p7i.vogel.de/wcms/75/c0/75c0d5ccd1cee4e66dbd5f3ed02efd0a/0129305300v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/9b/c1/9bc1caaaf2b30471c3d187069d2d8e4b/0129101585v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/9a/51/9a5199a5ad49e895b4aef7e04fe629e2/0129255110v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/d9/d6/d9d68c274ac9c3c728978fac46c773ba/0129239468v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/c3/53/c35394add74d23226fbd5c65833c0774/0129209052v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/63/9e/639e76b1a5edc6cb79a45b63aefadcfd/0129234417v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/0c/57/0c57cee9533d090c98061b4352d1103d/0129219561v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/ae/9a/ae9ad13f67e6dff52d1f20698c0edb64/0129210301v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/5f/54/5f545ab3a8bf940444930f98c9db8255/0129304670v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/69/1f/691f39ba12be3cad90eb88bdabc456a6/0127321404v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/6a/cc/6acc4f803241cfe5b6d60560c0a2b4d9/0126684948v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/ef/aa/efaae5a25fb0a4c55c434611033447af/0126532350v2.jpeg)
:fill(fff,0)/p7i.vogel.de/companies/69/72/69721860571ff/logo.jpeg)
:fill(fff,0)/images.vogel.de/vogelonline/companyimg/9700/9772/65.jpg)
:fill(fff,0)/p7i.vogel.de/companies/66/fa/66fa95f62cfdb/logo-positiv-rgb-276x106px.jpeg)
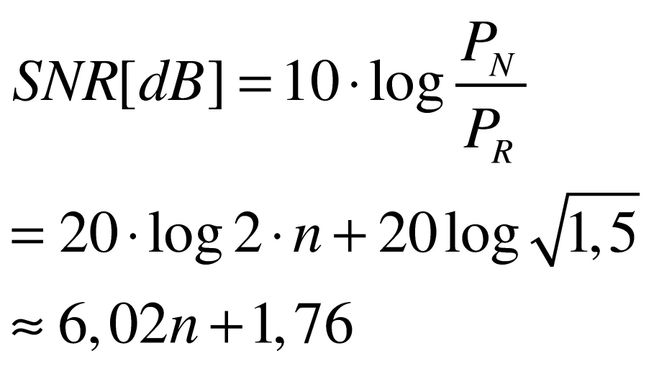
:quality(80)/p7i.vogel.de/wcms/48/32/48320991c9016c5e8d1c5d512598fe04/0125025724v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/de/48/de48603453b0bd091cef84dbbefe37c1/0126851659v2.jpeg)