Anbieter zum Thema
Detektion gestörter Signal- muster per Kreuzkorrelation
In der Messdatenauswertung müssen häufig bestimmte Signalmuster in einer empfangenen und durch Störungen überlagerten Signalfolge detektiert werden. Als Beispiel zeigt Bild 2 die von einem Sender ausgesandte Impulsfolge sowie das von einem Empfänger eingelesene gestörte Signal. Zum sicheren Herauslesen der Lage der Sendeimpulse aus dem Empfangssignal hilft die Kreuzkorrelationsfunktion (KKF). An Vorwissen ist seitens der empfangenden Messdaten-Applikation lediglich die grundsätzliche Form des Sendesignals notwendig. Im Beispiel handelt es sich um einen einfachen Rechteckimpuls, der als Abtastfolge xk intern vorgehalten wird. Man bildet nun die KKF, indem dieses xk mit der Empfangsfolge yk gemäß Formel 6:
verrechnet wird. Die Maxima der KKFi liegen an den Werten von i, um die yk verschoben werden muss, um eine größtmögliche Ähnlichkeit mit xk aufzuweisen. Durch Multiplikation dieses resultierenden Verschiebewerts i mit der Abtastzeit TA erhält man die zugehörige Zeitverschiebung. Das nach Anwendung der KKF sich ergebende Signal des Bildes zeigt drei deutliche Maxima und zwar an genau den Stellen, an denen auch die drei Sendeimpulse lagen.
Bei der Überwachung von technischen Systemen mit rotierenden Massen wie Werkzeugmaschinen, Fahrzeugantrieben oder Windrädern lassen sich erste Anzeichen einer Abnutzung in einem unrunden Lauf feststellen, der zu einem veränderten Schwingungsverhalten von Gehäusekomponenten führt. Man nimmt diese Schwingungen mit einem Sensor auf und führt sie der Messdaten-Applikation in abgetasteter Form zu.
Die Erfahrung zeigt, dass derartige Schwingungssignale einem Rauschsignal ähneln, in dem sich durch eine beginnende Abnutzung verursachte Änderungen in der Darstellung des Signals über der Zeit praktisch nicht detektieren lassen. Anders sieht es aus, wenn man die im Signal enthaltenen Frequenzanteile, sein Spektrum, analysiert. Hier zeigen sich recht schnell markante Änderungen.
Die zugehörigen Verfahren der Diskreten Fourier-Transformation (DFT) ermitteln aus N in einem Zeitfenster mit dem Abtasttakt TA gewonnenen Abtastwerten xi nun N Spektralwerte fk. fk ist dabei ein Vielfaches einer gedachten Grundfrequenz. Diese ist der Kehrwert der Zeitdauer des Fensters NTA. Für fk gilt also Formel 7:
Die DFT wird hierbei gemäß der Vorschrift nach Formel 8:
berechnet. Fast alle fertigen Funktionsbausteine führen die Berechnung ohne TA durch, so dass man in der Programmierung selbst hiermit noch multiplizieren muss. Bei genauerer Betrachtung fällt auf, dass diese Funktion periodisch mit der Periode N ist, sofern man die Beschränkung aufhebt, dass sie nur für ein k zwischen 0 und N - 1 berechnet wird. Weiterhin zeigt sich, dass sich die Spektralwerte zwischen 0 und N/2 im nachfolgenden Bereich zwischen N/2 und N-1 wiederholen, allerdings gespiegelt. Es lassen sich also „nur“ N/2 unabhängige Spektralwerte ermitteln.
(ID:44201748)





:quality(80)/p7i.vogel.de/wcms/59/bf/59bfd2822d711b0ae2cb9383b679f38d/0129302533v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/c1/94/c19403fe0194686b2f4911be7e1e9539/0129294209v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/e6/72/e67279e23a3267a463edf3e3f55c8e81/0129260553v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/cd/c2/cdc2463f324033ec22c60e74d983241c/0129371522v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/5c/4f/5c4f0eb073c372e2a494f37dd6783458/0129341654v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/28/0f/280fe550dfb032b53edbaac11d09bced/0129337134v3.jpeg)
:quality(80)/p7i.vogel.de/wcms/7b/57/7b5725dd2e7545ab4904a9b7a3735721/0129309389v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/b2/9c/b29ce10d1817d4b67968dfb737d812b7/0129308255v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/ac/a9/aca924f5aeb2280243c679915eb60213/0129344939v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/61/85/6185c7a5619aba866e3b237690bea839/0129334467v3.jpeg)
:quality(80)/p7i.vogel.de/wcms/3c/88/3c8863ad57e80adc0acb9c9d9ea30351/0129319571v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/4e/f2/4ef224fde728985d8b9630eb0fa37909/0129293948v3.jpeg)
:quality(80)/p7i.vogel.de/wcms/c7/f6/c7f61d0437c7f8fca3c6ff947ba2ad62/0129322490v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/66/0c/660c31afa35398bac9be42f2be73fdc4/0129073529v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/9c/35/9c35ed04fa562b190cbc496a695a6802/0128823288v1.jpeg)
:quality(80)/p7i.vogel.de/wcms/d7/e6/d7e6fe4124ec2efc726e9c3f2c2a4cfc/0128241940v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/e6/0a/e60ae162bd38bfc111ecf434d5c5fbd7/0129308123v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/75/c0/75c0d5ccd1cee4e66dbd5f3ed02efd0a/0129305300v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/a7/8c/a78c5f851db209abb1540909918fbf4a/0129260768v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/9a/51/9a5199a5ad49e895b4aef7e04fe629e2/0129255110v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/d9/d6/d9d68c274ac9c3c728978fac46c773ba/0129239468v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/d3/8b/d38b428f9a0a53319b1a54772f308d32/0129368862v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/bc/fc/bcfc3182c6e2422b82a9d0e1ce7dd945/0129336204v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/52/7a/527ad5ae7d10b9e34b72570639d7870c/plagiarius-zwerg-gnome-2849x1602v1.jpeg)
:quality(80)/p7i.vogel.de/wcms/c7/de/c7ded37e1a429fe2234da21e0c272a09/0129363486v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/43/43/4343a389b15f84f683b7d1cdb4745d23/0129331527v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/89/6b/896bbee46d0440c8a01ce4d0dab325f0/0129302555v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/69/1f/691f39ba12be3cad90eb88bdabc456a6/0127321404v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/6a/cc/6acc4f803241cfe5b6d60560c0a2b4d9/0126684948v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/ef/aa/efaae5a25fb0a4c55c434611033447af/0126532350v2.jpeg)
:fill(fff,0)/p7i.vogel.de/companies/63/88/63887b860cf66/me-logo-400px.jpeg)
:fill(fff,0)/p7i.vogel.de/companies/60/81/6081635146580/odu-logo-ohne-rgb.jpg)
:fill(fff,0)/p7i.vogel.de/companies/5f/15/5f157c2d880f4/ish-logo2020.jpg)
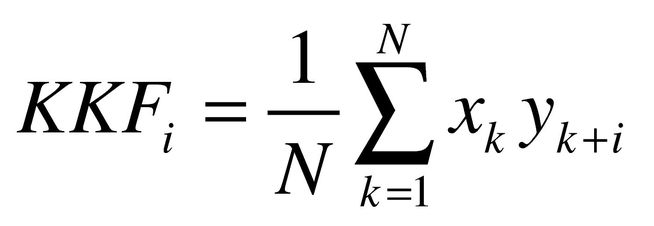
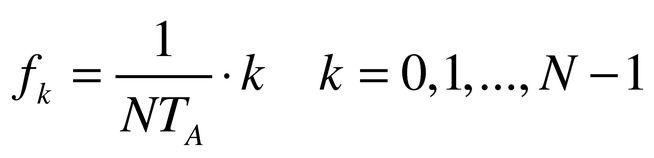
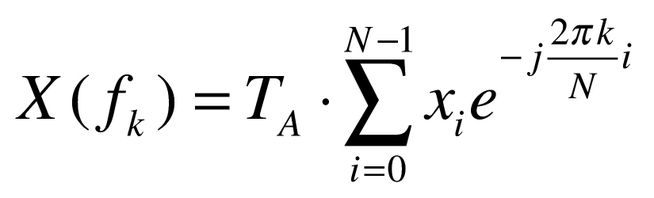
:quality(80)/p7i.vogel.de/wcms/48/32/48320991c9016c5e8d1c5d512598fe04/0125025724v2.jpeg)
:quality(80)/p7i.vogel.de/wcms/35/07/35071b4e9e1e377c4d10cc9e3b59f5cb/0128097510v2.jpeg)