Power-Tipps von TI, Teil 12 Maximieren des Wirkungsgrades von Stromversorgungen

In Tipp 11 haben wir gezeigt, wie sich Verlustquellen in Ihrer Stromversorgung mithilfe einer Taylorreihe ausfindig machen lassen. Im vorliegenden Beitrag wollen wir uns ansehen, wie man mit derselben Taylorreihe den Wirkungsgrad einer Stromversorgung in einem bestimmten Arbeitspunkt maximieren kann.

Anbieter zum Thema

ET System electronic GmbH

TRACO ELECTRONIC GMBH

MTM Power Messtechnik Mellenbach GmbH

Texas Instruments Deutschland GmbH

Im Power-Tipp Nr. 11 wurde vorgeschlagen, die Leistungsverluste als Funktion des Ausgangsstromes wie in Formel 1 zu berechnen.

Der nächste Schritt besteht nun darin, diesen einfachen Ausdruck in die Gleichung für den Wirkungsgrad einzusetzen, wie in Formel 2 zu sehen.

Anschließend lässt sich der Wirkungsgrad hinsichtlich des Ausgangsstromes optimieren (der Beweis sei dem Lernenden überlassen). Die Optimierung liefert ein interessantes Ergebnis. Ein maximaler Wirkungsgrad stellt sich ein, wenn der Ausgangsstrom gleich dem Ausdruck auf Bild Bild Formel 3 ist.

Als Erstes fällt auf, dass der a1-Term keinen Einfluss auf den Strom hat, bei dem der Wirkungsgrad seinen Spitzenwert erreicht. Das liegt daran, dass er sich auf Verluste bezieht, die proportional zum Ausgangsstrom sind, z. B. auf Verluste durch Diodenstrecken. Mit zunehmendem Ausgangsstrom steigen also diese Verluste und die Ausgangsleistung direkt, wodurch der Wirkungsgrad nicht beeinflusst wird.

Die zweite interessante Tatsache ist, dass sich der optimale Wirkungsgrad an einem Punkt einstellt, an dem die fixen Verluste und die Leitungsverluste gleich groß sind. Daraus folgt, dass eine Optimierung des Wirkungsgrades möglich sein muss, da man ja die Bauelemente wählen kann, durch welche die Werte von a₀ und a₂ festgelegt sind.

Gleichwohl sollte man sich auch bemühen, den Wert von a₁ zu senken, um den Wirkungsgrad zu steigern. Was man damit gewinnt, ist für alle Lastströme gleich, d. h. es findet keine Optimierung wie mit den anderen Termen statt. Das Ziel beim Term a₁ liegt darin, ihn möglichst zu minimieren und zugleich die Kosten der Lösung unter Kontrolle zu behalten.

Die Tabelle zeigt eine Zusammenfassung der verschiedenen Terme, die für die Verluste in Stromversorgungen relevant sind, und ihrer jeweiligen Verlustkoeffizienten. Sie soll einen Eindruck davon vermitteln, welche Kompromisse bei der Maximierung des Wirkungsgrades von Stromversorgungen unter anderem geschlossen werden müssen.

So wirkt sich beispielsweise die Wahl des On-Widerstands des Leistungs-MOSFETs auf den erforderlichen Gate-Ansteuerungsstrom, auf die Verluste durch die Ausgangskapazität (Coss) und möglicherweise auf die Verluste durch Überspannungs-Ableitelemente aus. Ein niedrigerer On-Widerstand bedeutet eine inverse Zunahme des Gate-Ansteuerungsstroms sowie der Coss- und Ableitelementeverluste. Man kann also a₀ und a₂ durch die MOSFET-Auswahl beeinflussen.

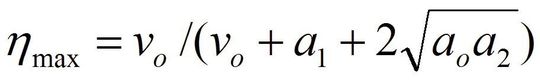
Die nächste Algebra-Aufgabe besteht darin, den optimalen Strom wieder in die Wirkungsgradgleichung einzusetzen und diese nach dem maximalen Wirkungsgrad aufzulösen. Siehe hierzu das Bild Formel 4.

(ID:26442960)