Hochgeschwindigkeitsapplikationen Genauigkeit von Simulationen quantifizieren

Die Hochgeschwindigkeits-Datenübertragung mit Datenraten bis 10 GBit/s oder mehr stellt die Entwickler von Steckverbindern vor harte Vorgaben. Hier ist die elektromagnetische Simulation dreidimensionaler Bauelemente ein unentbehrliches Hilfsmittel. Der Beitrag beschreibt, wie eine akkurate elektromagnetische Simulation zu einem funktionierenden Design mit minimalem Prototypenaufwand führt.

Anbieter zum Thema

MES Electronic Connect GmbH & Co. KG

ept GmbH

CADFEM Germany GmbH

Moderne Datenübertragungssysteme stellen Elektronikentwickler vor neue Herausforderungen. Die Datenübertragung erfolgt nicht mehr über parallele Bussysteme, die Tendenz geht zur seriellen Hochgeschwindigkeitsübertragung. Standards wie Gigabit Ethernet (IEEE 802.3ab, -ae,-an), PCI Express 3.0 oder serial ATA (SATA) spezifizieren Datenraten bis 10 GBit/s. Andere High-Speed-Telekommunikationsstandards erhöhen die Bandbreite existierender Hardware über deren ursprünglich gedachten Gebrauch hinaus.

Die Spezifikation KAT.-6 für Twisted-Pair-Leitungen schreibt eine Isolation zwischen den Kabeln von weniger als –80 dB vor. Diese strengen Vorgaben führen zu harten Anforderungen für den Abschlusswiderstand des RJ45-Steckverbinders und den Übergang zum Kabel. Diese Forderungen sind nicht nur in den Fertigungstoleranzen, sondern auch in der Design Methodologie festgeschrieben. Insbesondere ist eine genaue elektrische Analyse kritischer Komponenten notwendig, um die Entwicklung mit kurzen Markteinführungszeiten abzuschließen.

Typischer serieller Hochgeschwindigkeitskanal

Der Schaltplan eines typischen Hochgeschwindigkeitskanals ist in Bild 1 dargestellt. Dieses Modell umfasst zwei benachbarte serielle Kanäle. Eine Bit-Sequenz wird in einen Puffer gespeist, der wiederum den physikalischen Kanal treibt. Das Modell des physikalischen Kanals kann aus verschiedenen Übergängen wie Steckverbindern, Gehäusen, Vias oder Bonddrähten mit untereinander verbundenen Übertragungsleitungen bestehen.

Die Qualität eines Kanals lässt sich durch Eigenschaften aus dem Zeitbereich wie Augendiagramm, Bitfehlerrate oder Jitter charakterisieren. Die meisten Standards schreiben auch Auflagen im Frequenzbereich vor. Die Frequenzbereichsanalyse ist in der Regel sehr schnell durchzuführen und offeriert deshalb ein effizientes Hilfsmittel für statistische Untersuchungen oder Optimierungsaufgaben. Daher sollte eine Simulation eines High-Speed-Kanals in einer Umgebung stattfinden, die sowohl die Frequenz- als auch Zeitbereichsanalyse berücksichtigt. Dieser Ansatz wurde anhand eines detaillierten Fallbeispiels für einen 10 GBit/s Ethernet-Kanal im Bladeserver von IBM auf der DesignCon 2008 [1] präsentiert.

Der nachfolgende Abschnitt beschreibt, wie die elektromagnetische Simulation genutzt werden kann, um genaue Modelle der dreidimensionalen Bereiche zu generieren, die dann in die Simulation des High-Speed-Kanals implementiert werden.

3-D-Simulation elektromagnetischer Bauelemente

Dreidimensionale Komponenten wie Steckverbinder, Vias, Bonddrähte oder die Ausführung der Signale aus einem Gehäuse spielen eine entscheidende Rolle für die Signalintegrität eines Kanals. Ungewünschte Reflexionen, Übersprechen oder Gleichtaktwandlung (common mode conversion) können katastrophale Auswirkungen auf die Systemleistung haben. Deswegen sind genaue elektrische Modelle für diese Komponenten essenziell. Derartige Modelle erhält man entweder durch sorgfältige Messungen der elektrischen Parameter isolierter Bauelemente oder durch Simulation der Bauelemente in einem dreidimensionalen Feldsimulator. Der Entwickler, der danach das Modell verwendet, muss beide Lösungswege sehr gut kennen. Simulationsmethoden haben eine Reihe von Vorteilen gegenüber der Messung.

Die Analyse von Bauelementen mittels elektromagnetischer Simulation wird oft als „virtuelles Prototyping“ bezeichnet. Die Zykluszeit, die für das virtuelle Prototyping benötigt wird, ist wesentlich geringer als der Aufbau von Prototypen, da keine Hardware erstellt werden muss.

Darüber hinaus kann die Abhängigkeit der elektrischen Parameter vom Werkstoff und der Geometrie mit wenig Aufwand in kurzer Zeit ermittelt werden. Der Grundlage, um elektromagnetische Komponenten in High-Speed-Systemen genau zu simulieren, bildet die korrekte Lösung der Maxwellschen Gleichungen. Versteht der Entwickler das Konvergenzkonzept, kann er die elektromagnetische Analyse getrost anwenden.

3-D-Strukturen mit Maxwell‘schen Gleichungen rechnen

Die Maxwell‘schen Gleichungen beschreiben die elektrischen Parameter jeglicher Struktur sofern die Werkstoffparameter und die exakte Geometrie bekannt sind. In der Praxis ist die exakte Lösung der Maxwell‘schen Gleichungen nur für einige einfache Strukturen möglich. Deshalb wurden numerische Näherungsverfahren entwickelt. Diese werden heute weitgehend genutzt, um beliebige dreidimensionale Strukturen zu rechnen. Die am weitesten verbreiteten Methoden sind die der Finiten Differenzen im Zeitbereich (Finite Difference Time Domain – FDTD) und die der Finiten Elemente (FEM).

Sowohl bei FDTD als auch FEM werden die Maxwell‘schen Gleichungen dadurch gelöst, dass das Modell in kleine Teilstücke (Sub-Domänen) unterteilt und lokal für jeden Bereich der Domäne die Feldlösung angenähert wird. Die Näherungslösung führt zu einem System algebraischer Gleichungen, die mithilfe eines Computers gelöst werden können. Die fundamentale Frage, die der Entwickler beantworten muss, bevor er die Ergebnisse verwendet, ist „wie genau ist die Lösung?“. Da numerische Verfahren nur Näherungslösungen sind, ist dieser Punkt sehr wichtig.

Konvergenz numerischer Verfahren

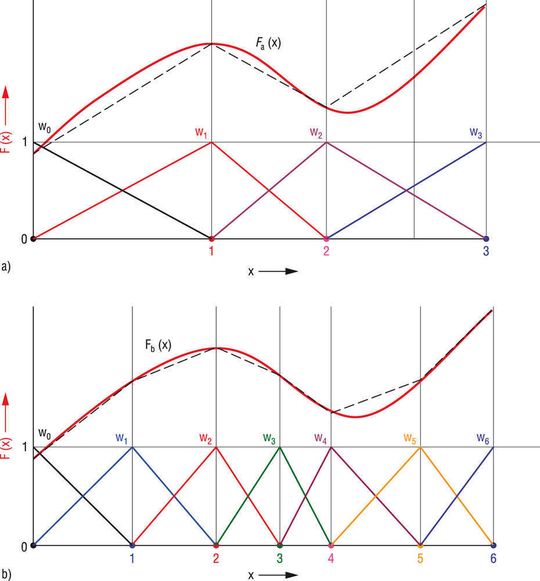
Das Konzept der „Konvergenz“ ist unerlässlich, um zu verstehen, wie die Genauigkeit von numerischen Verfahren objektiv beurteilt werden kann. Die einfache eindimensionale Funktion, die in Bild 2a dargestellt ist, soll diesen Gedanken verdeutlichen. Die rote Kurve, beschrieben durch die Funktion F(x), wird stückweise durch die stetigen Basisfunktionen w0 bis w3 angenähert. Die Näherungslösung ist Fa(x). Jede dieser Basisfunktionen ist endlich nur in einem begrenzten Bereich und wird null an der nächsten Stützstelle. Die einzelnen Basisfunktionen sind „erster Ordnung“, d.h., sie werden durch eine lineare örtlich begrenzte Funktion beschrieben. Für Basisfunktionen höherer Ordnung werden Polynome höherer Ordnung verwendet, wodurch die lokale Näherung genauer wird, aber auch die Anzahl der unbekannten Koeffizienten pro Element steigt. Das in Bild 2 dargestellte Szenario beschreibt die eindimensionale Näherungslösung aus der Finiten Elemente Methode unter Verwendung einer Basisfunktion erster Ordnung. Für eine detailliertere Darstellung numerischer Methoden in der elektromagnetischen Analyse sei auf [2,3] verwiesen.

In Bild 2b sind dieselbe Funktion F(x) und die Näherungslösung Fb(x) zu sehen, bei der eine größere Anzahl von Basisfunktionen verwendet wurde. In diesem Fall wurde der Bereich in kleinere Stücke unterteilt, die Genauigkeit ist im Vergleich zu Bild 2a höher. Numerische Verfahren konvergieren, wenn die Näherungslösung die exakte Lösung anhand unendlich kleiner Sub-Domänen erreicht. Dieser Gedanke erscheint im Fall von Bild 2 trivial, aber bei großen, komplexen dreidimensionalen Modellen wird dies kritisch, da jedes Element in der Domäne feste „numerische Kosten“ hat. D.h., die Anzahl der Unbekannten im Gleichungssystem ist proportional zur Anzahl der Sub-Domänen oder Elemente. Deswegen ist es nicht nur wichtig, dass die Lösung konvergiert, sondern dies mit der kleinstmöglichen Anzahl von Elementen geschieht.

Verifikation durch eine von der ACES durchgeführten Teststudie zum Störschutz

Das Konvergenzkonzept muss bei der dreidimensionalen Finiten Elemente Methode sehr sorgfältig ausgeführt werden. Eine Teststudie (Bild 3) der Applied Computational Electromagnetic Society (ACES) [4] soll zeigen, wie das Konvergenzkonzept verwendet werden kann, um die Genauigkeit der numerischen Lösung zu quantifizieren. Der erste Schritt besteht darin, die Modelldomäne in Tetraeder-Bausteine zu unterteilen. Die Basisfunktionen werden in der gleichen Weise wie in Bild 2 örtlich begrenzt. Die gesuchte Größe ist die Leistung, die in den Hohlraum von der Koaxialleitung eingekoppelt wird.

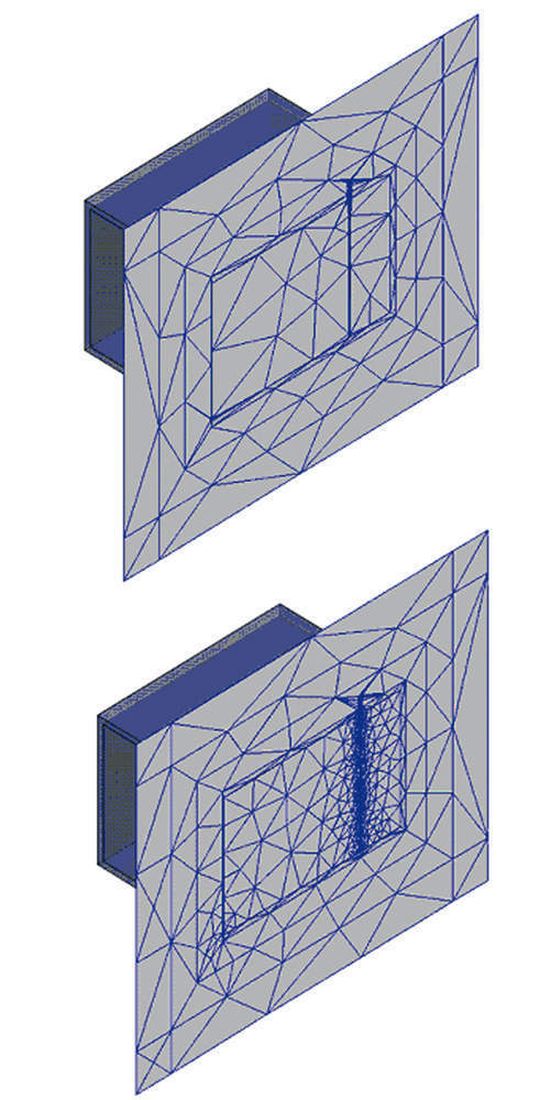
Bild 5 oben zeigt einen Querschnitt des Modells mit der ursprünglichen Diskretisierung. Die Dreiecke im Querschnitt sind die Oberflächen der dreidimensionalen Tetraeder. Da die Tetraeder einem dreidimensionalen Netz ähneln, wird diese Diskretisierung oft als „Netz“ bezeichnet. Die Lösung der Maxwell‘schen Gleichungen, die mit dieser groben Vernetzung erzielt wird, ist relativ ungenau, ähnlich Bild 2a. Nichtsdestotrotz wurde diese Lösung bei minimalen „numerischen Kosten“ aufgrund der kleinen Anzahl von Unbekannten erzielt.

Ein hochentwickelter Fehlerabschätzungsalgorithmus [5] kann nachfolgend verwendet werden, um den lokalen Fehler in jedem Tetraeder zu berechnen. Das Netz wird dann in den Regionen verfeinert, in denen der Fehler am größten ist. Neue Stützstellen werden in der Domäne strategisch platziert und das Feld wird im verfeinerten Netz erneut berechnet. Dieser Ablauf wird so lange wiederholt, bis die fortlaufenden Lösungen in verschiedenen Netze das gleiche Ergebnis innerhalb eines vorgegebenen Genauigkeitsbereiches erzielen. Dieser Prozess ist als adaptive Verfeinerung bekannt und im Flussdiagramm in Bild 4 dargestellt.

Bild 5 unten zeigt das endgültige Netz, das für diesen Testfall errechnet wurde. Das Netz ist sehr feinmaschig in der Nähe der Drähte und deren Abschluss. Man sollte sich an dieser Stelle immer bewusst sein, dass grundsätzlich in allen numerischen Verfahren das Netz gelöst wird und nicht die darunter liegende Geometrie.

Die Herausforderung besteht darin, ein geometrisch getreues und elektromagnetisch adäquates Netz zu bilden, das das darunter liegende Modell genau repräsentiert. Die Genauigkeit dieser Methode ist in Bild 6 unterlegt, das die veröffentlichten ACES-Daten für den Testfall zusammen mit den sequenziellen Lösungen der verfeinerten Netze zeigt. Die Möglichkeit, die Genauigkeit quantitativ zu spezifizieren, sichert die Vertrauenswürdigkeit der endgültigen Lösung ab.

Fallbeispiel Simulation eines RJ45-Steckverbinders

Die KAT.-6-Richtlinie für Twisted-Pair-Leitungen gibt strikte Vorgaben hinsichtlich der Kabelsteckverbinder. Insbesondere die Isolation zwischen den Paaren, die durch einen Steckverbinder verlaufen, stellt eine große Herausforderung für den Entwickler dar. Die Leistungsfähigkeit des Steckverbinders kann mithilfe elektromagnetischer 3-D-Simulation vorhergesagt werden. Sofern notwendig lässt sich das Design beim virtuellen Prototyping noch vor der Fertigung ändern.

Bevor ein Modell für die Simulation angefertigt wird, sollten ein paar praktische Überlegungen durchgeführt werden. Als erstes muss eine genaue geometrische Beschreibung des Modells für die Netz-Algorithmen zur Diskretisierung zur Verfügung stehen. Dieses geometrische Modell kann direkt über eine Preprozessor-Schnittstelle gezeichnet werden oder existierende CAD-Daten werden in den Simulations-Preprozessor importiert.

Nachdem das geometrische Modell festgelegt ist, müssen die Werkstoffeigenschaften, die Randbedingungen und Quellen spezifiziert werden. Werkstoffeigenschaften werden meist von den Anbietern zur Verfügung gestellt, sollten aber kritisch überprüft werden, wenn man sie für die elektromagnetische Simulation verwendet. Vorsicht ist insbesondere dann geboten, wenn die gewünschten elektrischen Parameter stark von den Werkstoffeigenschaften abhängen. Langjährige Praxiserfahrungen haben ergeben, dass die meisten Unstimmigkeiten zwischen einer FEM-Simulation mit adaptiver Verfeinerung und Messung auf Diskrepanzen zwischen der Modellgeometrie und dem tatsächlichem Bauteil sowie nicht korrekter Werkstoffparameter zurückzuführen sind. Messfehler, meist aufgrund falscher Einbaubedingungen, sind ein weiterer gängiger Grund für die Unstimmigkeiten.

S-Parameter ermitteln

Sind die Geometrie, Modellparameter, Eingangs- und Ausgangskanäle (d.h. Quellen) festgelegt, kann die Simulation entsprechend des Flussdiagramms in Bild 4 erfolgen. Eine typische Konvergenzkurve zeigt Bild 7, das die maximale Änderung aller S-Parameter als Funktion der adaptiven Durchgänge darstellt. In den meisten Fällen sind die maßgeblichen Parameter, die aus der Simulation extrahiert werden, die S-Parameter. Wird die Simulation dazu genutzt, andere elektrische Parameter vorherzusagen, sollten die Konvergenzkriterien dementsprechend definiert werden.

Der erste Messwert in der Konvergenzkurve in Bild 7 beginnt bei der zweiten Lösung, da dieser die Änderung von der ersten zur zweiten Lösung repräsentiert. Da das Netz durch die adaptive Verfeinerung verbessert wird, wird die Abhängigkeit der Lösung vom Netz geringer, bis das Fehlerkriterium erfüllt ist.

In Bild 8 ist das Nahbereichsübersprechen verschiedener KAT.-6-RJ45-Steckverbinder von Molex mit den Simulationsdaten des nominalen Steckverbinders dargestellt. Diese Werte belegen nicht nur die Genauigkeit der Simulation, sie zeigen auch den großen Dynamikbereich auf, der mithilfe der elektromagnetischen Simulation erzielbar ist. Die Messungen wurden gemäß IEC 60603-7-5 durchgeführt [6].

Fazit

Hochgeschwindigkeits-Datenkommunikationsysteme setzen strikte Anforderungen hinsichtlich der elektrischen Eigenschaften passiver Verbindungselemente für die Datenkommunikation. Die elektromagnetische Simulation dreidimensionaler Bauelemente ist ein unentbehrliches Werkzeug für die erfolgreiche und zeitgerechte Entwicklung von Transmissionskanälen in Hochgeschwindigkeitssystemen. Die Zuverlässigkeit der elektromagnetischen Analyse wird durch die Kontrolle der Lösungskonvergenz abgesichert, mit der die Genauigkeit der Lösung spezifiziert werden kann.

*Dr. Devin Crawford arbeitet als Applikationsingenieur bei Ansoft in München. Dr. Matthew Commens ist als Technical Director für HF-Produkte bei Ansoft, LLC in Pittsburgh, PA (USA) tätig.

(ID:271045)