Entwurf optimierter EMV-Filter für die Praxis

Anbieter zum Thema

MES Electronic Connect GmbH & Co. KG

CADFEM Germany GmbH

Würth Elektronik eiSos GmbH & Co. KG

DCC Dirks Compliance Consulting

Einfügungsdämpfung ist lastabhängig

Doch zurück zu unserem „klassischeren“ Filter, der aus drei Kondensatoren von 100 nF im Querzweig und einer Drossel 742792093 im Längszweig besteht, und dessen Einfügungsdämpfung in Bild 4 und 5 zu sehen ist. Vereinfacht gesagt gibt die Einfügungsdämpfung an, wie viel weniger Leistung in der Last aufgrund des eingefügten Filters umgesetzt wird.

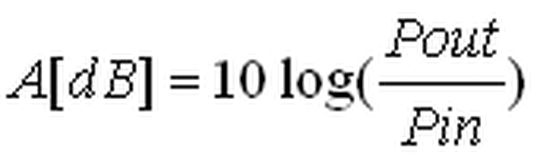
Betrachtet man die Formel der Einfügungsdämpfung [Gleichung 1] ist sofort ersichtlich, dass neben der Impedanz des Filters auch die Quell- und Lastimpedanz das Ergebnis beeinflussen (POUT = UOUT2/ZOUT).

Bei Messgeräten wie dem Networkanalyzer hat sich als Industriestandard die Konvention durchgesetzt, als Quell- und Lastimpedanz gleichermaßen R = 50 Ω zu verwenden. Sinnvollerweise wird diese Vereinbarung auch bei der Simulation von Filtern zugrunde gelegt. Die Quell- und Lastimpedanzen, die EMV-Filter in ihrer späteren Applikation vorfinden, sind in aller Regel verschieden und außerdem keineswegs 50 Ω, sondern irgendeine (komplexe) Impedanz.

Das bedeutet aber, dass es nur dann möglich ist, die Einfügungsdämpfung eines Filters vorherzusagen, wenn die realen Abschlüsse ZIN(f) und ZOUT(f) bekannt sind. Für Hersteller von EMV-Filtern beispielsweise kann diese Bedingung praktisch nie erfüllt werden, da der Hersteller ja gar nicht wissen kann, in welcher Umgebung der Kunde seinen Filter später einsetzt.

Deshalb ist es durchaus üblich, Filter-Dämpfungskurven für ZIN = ZOUT = 50 Ω anzugeben, und damit zumindest eine gewisse Vergleichbarkeit der Filter untereinander zu ermöglichen. Dabei bleibt leider „der schale Nachgeschmack“, nicht wirklich zu wissen, was der Filter tatsächlich für einen Dämpfungsverlauf leisten wird. Um sich einen Eindruck davon machen zu können, was einen schlimmstenfalls erwarten könnte, wurde in CISPR 17 die so genannte „Approximate Worst Case Method“ definiert. Diese sieht vor, den Filter in zwei verschiedenen Abschluss-Kombinationen zu betrachten:

1. ZIN = 0,1 Ω, ZOUT = 100 Ω

2. ZIN = 100 Ω, ZOUT = 0,1 Ω

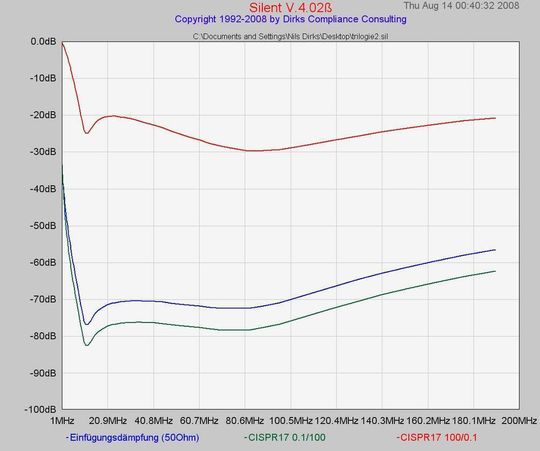
Bei Filtern, die beispielsweise nur aus einer einzelnen Längs-Drossel bestehen ergibt sich für beide Fälle derselbe Dämpfungsverlauf; der Filter ist symmetrisch. Da sich durch den Einsatz eines Querzweiges, wie beispielsweise in Form eines Kondensators, deutlich höhere Dämpfungswerte erzielen lassen, ist eine L-Struktur – wie bei den SILENT-Filtern - sehr gebräuchlich. Bei dieser Art von Filtern zeigt sich dann allerdings ein dramatischer Unterschied zwischen den beiden CISPR-17-Dämpfungsverläufen (Bild 7).

Einfluss der Abschlüsse auf das Verhalten

Während die 0.1/100-Kurve sogar noch etwas höhere Dämpfungswerte verspricht, ist die Dämpfung der 100/0.1-Kombination rund 50 dB schlechter als der 50-Ω-Verlauf. Mit Blick auf die Filterschaltung in Bild 1 ist das leicht nachzuvollziehen: Der Filterabschluss (Lastimpedanz) von 0.1 Ω ist zu den Kondensatoren parallel geschaltet. Ist nun bei einer betrachteten Frequenz die Impedanz der Kondensatoren größer als die 0.1 Ω der Last, fließt der größere Teil des Stromes durch die Last und setzt dort entsprechend eine POUT [Gleichung 1] um. Im umgekehrten Fall, also mit einer Lastimpedanz von 100 Ω, sind die Kondensatoren vergleichsweise sehr niederohmig, so dass der Großteil des Störstromes durch diese, und nicht durch die Last fließt.

Dieser Zusammenhang lässt sich eindeutig zeigen: Die Drossel ohne Querzweig liefert eine Dämpfung von –20 dB etwa bei 40 und 190 MHz (Bild 6). Betrachtet man im Bild 7 die Dämpfungs-Differenz zwischen der 50-Ω-Kurve (blau) und dem 100/0.1-Fall (rot), stellt man fest, dass dieser „Fehlabschluss“ bei 40 MHz zu einem Rückgang der Dämpfung um ca. 48 dB, bei 190 MHz jedoch nur um ca. 36 dB führt. Da die Drossel auf beiden Frequenzen den gleichen Dämpfungswert zeigt, ist die Differenz von ca. 12 dB auf den Querzweig zurückzuführen. Dieser ist bei niedrigeren Frequenzen, wie bei 40 MHz, sehr viel niederohmiger als bei höheren Frequenzen ab 190 MHz und leistet daher bei niedrigen Frequenzen einen größeren Beitrag zur Gesamtdämpfung. Wird der Querzweig nun durch den parallel geschalteten 0,1-Ω-Abschluss weitgehend unwirksam gemacht, ist der Schaden folglich bei niedrigeren Frequenzen besonders groß.

Dämpfungswerte erhöhen

Aus dieser Erkenntnis lassen sich mehrere konkrete Handlungsempfehlungen ableiten:

• Der Dämpfungsverlauf aus dem Datenblatt ist mit Vorsicht zu genießen!
• Wird eine L-Filterstruktur verwendet, ist darauf zu achten, dass der Kondensator-Querzweig auf der Seite des Filters liegt, wo die höhere Abschlussimpedanz erwartet wird.
• Die „sichere Wette“: Möchte man sich mit den Abschlussimpedanzen gar nicht befassen oder ist eine Messung/Abschätzung nicht möglich, wird der Filter zu einer T-Struktur mit einer weiteren Drossel gleichen Typs erweitert. Dadurch erhöhen sich die Dämpfungswerte nochmals, vor allem aber ist der Filter tolerant gegenüber niederohmigen Abschlüssen. Dieser Ansatz spart Entwicklungsaufwand zu Lasten der dadurch höheren Stückkosten und wird sich somit für größere Serien nicht empfehlen.

Der Vollständigkeit halber sei erwähnt, dass es insbesondere bei Produkten, die später in größeren Stückzahlen gefertigt werden sollen, durchaus sinnvoll sein kann, die Abschlüsse in der realen Baugruppe messtechnisch oder per Simulation zu ermitteln. Mit geeigneter Simulationssoftware kann dann ein sowohl leistungs- als auch kostenoptimierter Filter passgenau für die reale Betriebsumgebung entwickelt werden

Quellennachweis:

[1] „EMV-Filterentwurf mit der Drosseldatenbank“, Prof. Chr. Dirks, U. Margieh, Elektronik 4/92, S.110 ff

[2] „EMV beginnt auf der Leiterplatte“, Nils Dirks, Elektronik 26/07, S. 48ff und Elektronik 01/08, S.56ff

[3] www.software-silent.de

[4] Datenblatt Würth: http://www.wuerth-elektronik.de/eisos/pdf/742792093.pdf

[5] „Die Mär vom Plattenkondensator, Nils Dirks, ELEKTRONIKPRAXIS Sonderheft 2/2005, S. 42ff

*Nils Dirks ist Inhaber der Dirks Compliance Consulting in Herrsching bei München.

(ID:280719)