Uhrenquarze Anwendungsbetrachtungen und Effekte der Miniaturisierung

Elektronische Geräte werden trotz kontinuierlich erweiterter Funktionalität immer kleiner. Dies ist nur mit ebenfalls stark verkleinerten Komponenten und Bauteilen möglich. Die Komplexität konventioneller Quarze wird häufig unterschätzt, doch die Miniaturisierung stellt speziell diesen Bereich des Bauteilemarktes vor große Herausforderungen.

Anbieter zum Thema

Jauch Quartz GmbH

GLYN GmbH & Co. KG

Keysight Technologies Deutschland GmbH

Epson Europe Electronics GmbH

Schaltungstechnisch lässt sich ein Schwingquarz als in Reihe geschaltete Induktivität, Kapazität und Widerstand mit diesem Zweig parallel geschalteter Kapazität des Quarzgehäuses betrachten (Bild 1). Der im Schwingkreis enthaltene Widerstand, welcher typischerweise mit ESR oder CI bezeichnet wird, repräsentiert die Dämpfung des Quarzes, also seinen „Verlust“.

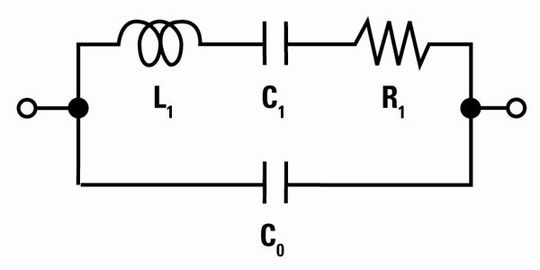
Um den Quarz in Schwingung zu halten, ist es notwendig, die im Serienwiderstand verlorengehende Energie permanent nachzuliefern, was durch einen im Oszillatorschaltkreis (Halbleiter, an den der Quarz angeschlossen ist) befindlichen Verstärker – auch häufig als „negativer Widerstand“ oder „–R“ bezeichnet – realisiert wird.

Um das Anschwingen sicherzustellen, ist es jedoch notwendig, dem Quarz deutlich mehr Energie zuzuführen als er für die reine Aufrechterhaltung der Oszillation benötigt. Als Faustregel kann hier der Faktor 5 bis 10 gelten. Je höher dieser Wert ist desto schneller schwingt der Quarz an, desto mehr Strom benötigt jedoch auch der Oszillationsschaltkreis, was speziell in batteriebetriebenen Anwendungen nicht gewünscht ist. Wird dieser Faktor zu hoch gewählt, also deutlich mehr als das zehnfache der im Serienwiderstand absorbierten Energie zugeführt, kann dies zu einer „Übersteuerung“ des Quarzes führen. Das heißt, der Quarz wird so stark angeregt, dass seine mechanische Schwingung Amplituden erreicht, die den Quarz an das Gehäuse anschlagen lassen und ihn damit mechanisch beschädigen.

(ID:311847)