Serie A/D-Wandler: Die Parameter THD, THD + N und SFDR Dynamische Leistungsfähigkeit von A/D-Wandlern, Teil 1

Die sechs Spezifikationen SINAD, SNR, THD, THD + N, SFDR und ENOB kennzeichnen die dynamische Leistungsfähigkeit von A/D-Wandlern. Leider sind diese Werte nicht konsequent in den Datenblättern aufgeführt. Für einen Vergleich unterschiedlicher Wandler ist es hilfreich, die Zusammenhänge zwischen diesen sechs Parametern zu kennen.

Anbieter zum Thema

TRACO ELECTRONIC GMBH

Bicker Elektronik GmbH

RECOM Power GmbH

Analog Devices

Sechs gängige Begriffe, die die dynamische Leistungsfähigkeit von A/D-Wandlern beschreiben, sind SINAD (Signal-/Rausch- und Verzerrungsverhältnis), ENOB (effektive Bitanzahl), SNR (Signal/Rausch-Verhältnis), THD (gesamte harmonische Verzerrung), THD + N (gesamte harmonische Verzerrung plus Rauschen) und SFDR (störungsfreier Dynamikbereich). Obwohl die meisten Hersteller von A/D-Wandlern die gleichen Definitionen für diese Spezifikationen verwenden, sind die Werte nicht konsequent in den Datenblättern angegeben. Beim Vergleich von A/D-Wandlern ist es wichtig, nicht nur zu verstehen, was spezifiziert wird, sondern auch die Zusammenhänge zwischen den Spezifikationen zu kennen. Teil 1 dieses Beitrags geht auf die Begriffe SNR, THD, THD + N und SFDR ein. Im zweiten Teil werden SINAD und ENOB erläutert.

Fourieranalyse bildet die Grundlage der Fehlerabbildung

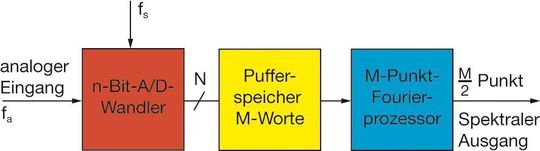
Es gibt eine Reihe von Möglichkeiten, um die Verzerrungen und das Rauschen eines A/D-Wandlers zu quantifizieren. Diese Möglichkeiten basieren auf Fourieranalysen, die mit einem standardisierten Testaufbau nach Bild 1 durchgeführt werden.

Das Ausgangsspektrum einer FFT-Analyse (Fast-Fourier-Transformation) ist eine Serie von M/2-Punkten im Frequenzbereich (M ist die Anzahl der Fourierfunktionen – die Anzahl an Samples im Pufferspeicher). Die Abstände zwischen den Punkten betragen fs/M. Der insgesamt abgedeckte Frequenzbereich reicht von DC bis fs/2, mit fs als Abtastrate. Die Breite jedes „Bins“ (die Daten eines Kanals, manchmal auch als Auflösung der Fouriertransformation bezeichnet) ist fs/M.

Bild 2 zeigt eine FFT-Analyse für einen idealen 12 Bit A/D-Wandler mit dem Programm ADIsimADC von Analog Devices. Zu beachten ist, dass das theoretische Grundrauschen der FFT so groß ist wie das theoretische Signal-Rausch-Verhältnis (SNR) plus FFT-Prozessverstärkung (10 · log (M/2)).

Es ist wichtig, daran zu denken, dass der Wert für das Rauschen in der SNR-Berechnung dem Rauschen entspricht, welches sich über die gesamte Nyquist-Bandbreite (DC bis fs/2), erstreckt.

Die Fouriertaransformation verhält sich jedoch als schmalbandiger Spektrumanalysator mit einer Bandbreite von fs/M, welche das Spektrum überstreicht. Dies hat den Effekt, dass das Rauschen um einen Wert, der der Prozessverstärkung entspricht, unterdrückt wird. Dies ist der gleiche Effekt wie bei der Verkleinerung der Bandbreite eines analogen Spektrumanalysators.

Mittelwert mehrerer Fouriertransformationen

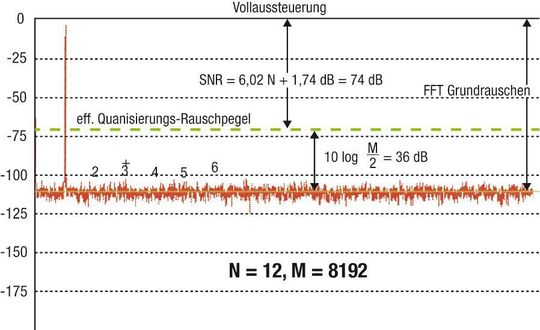
Die in Bild 2 gezeigten FFT-Daten repräsentieren den Durchschnitt von fünf einzelnen Fouriertransformationen. Zu beachten ist, dass sich der Mittelwert mehrerer Fouriertransformationen nicht auf das durchschnittliche Grundrauschen auswirkt. Es glättet lediglich die zufälligen Abweichungen in den Amplituden jedes Frequenz-Bins.

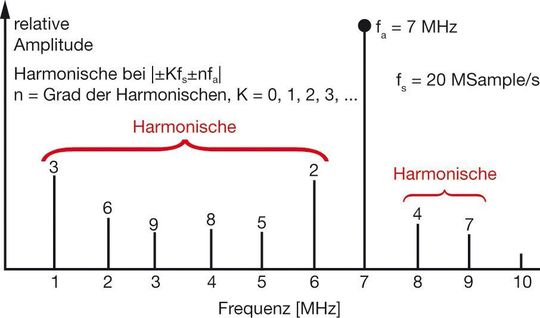
Die FFT-Analyse kann wie ein analoger Spektrumanalysator verwendet werden, um die Amplitude der verschiedenen Harmonischen sowie der Rauschkomponenten eines digitalisierten Signals zu messen. Die Harmonischen des Eingangssignals können von anderen Verzerrungsprodukten durch ihre Lage im Frequenzspektrum unterschieden werden. Bild 3 zeigt ein Eingangssignal von 7 MHz, abgetastet mit 20 MSample/s und die Lage der ersten neun Harmonischen. Gespiegelte Harmonische von fa fallen auf Frequenzen von |±Kfs ± nfa| mit n als Ordnung der Harmonischen und K = 0, 1, 2, 3, .... Die Harmonischen zweiter und dritter Ordnung sind normalerweise die einzigen, welche im Datenblatt spezifiziert sind, weil sie meist die größten sind. In einigen Datenblättern wird auch der Wert der schlechtesten Harmonischen angegeben.

(ID:342969)