Auflösung von Winkelmessungen erhöhen

Anbieter zum Thema

Micro-Epsilon Messtechnik GmbH & Co. KG

EBV Elektronik GmbH & Co. KG

IBR Leiterplatten GmbH & Co. KG

ic-Haus/ HT-Analyst HT-Analyst

iC-Haus GmbH

Systemvergleich: Absolute optische Encoder

Optische Drehgeber nutzen eine präzise Maßverkörperung und profitieren von der System-on-Chip Integration bezüglich Auflösung und kleiner Bauform. Dabei werden neben mehrspuriger Abtastung digitaler Codes analoge Signale interpoliert, um Zwischenwerte zu generieren.

Nach dem Durchlichtverfahren aufgebaute optische Geber arbeiten mit einer LED als Beleuchtung, einer Codescheibe mit mehreren Spuren sowie einem lichtempfindlichen Sensor-IC, der sowohl den Photodetektor, die Signalaufbereitung als auch Schaltkreise zur Interpolation in einem System-on-Chip kombiniert.

Standardtechnik mit digitalem Absolutcode

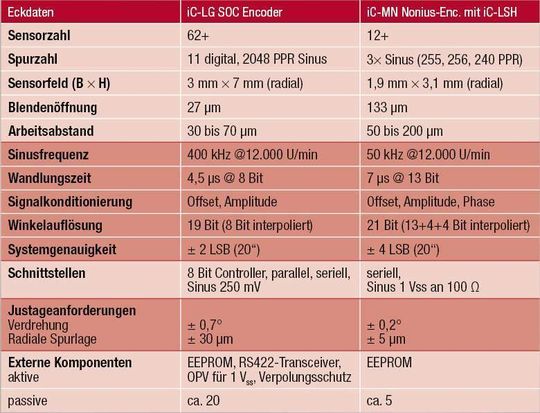
Eine sehr feine Grundauflösung wird durch eine hohe Anzahl von Teilungsperioden erzielt, die auf den Umfang der Codescheibe verteilt sind. So unterteilt beispielsweise der System-On-Chip Positionssensor iC-LG eine Umdrehung zunächst in 2048 gleiche Intervalle. Bei einer Codescheibe mit einem Durchmesser von 42 mm ergeben sich somit Strukturbreiten auf der Codescheibe um 27 µm.

Um über eine volle Umdrehung die absolute Position zu erhalten, müssen die Teilungsperioden voneinander unterschieden werden. Dazu dienen bis zu 13 weitere Spuren auf der Codescheibe, die einen digitalen Absolutcode liefern, als eindeutige Information über das Intervall.

Die weitere Verfeinerung der Position wird durch Interpolation der Teilungsperioden erreicht, wofür jede Teilung ein Sinus- sowie Cosinus-Signal bereitstellt. Durch die Berechnung der Tangensfunktion lässt sich hieraus der momentane Phasenwinkel innerhalb eines Intervalls bestimmen. Dieser kann dann mit dem digitalen Absolutcode verrechnet werden, um eine weitaus feinere absolute Positionsinformation von bis zu 21 Bit zu erhalten.

Nonius-Methode für eine feinere Auflösung

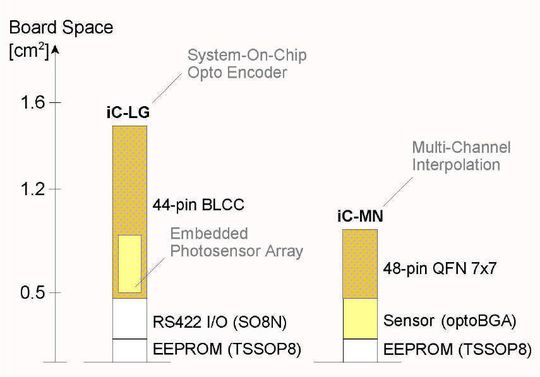
Bild 4: Ein Verzicht auf digitale Absolutcodes halbiert den Platzbedarf und ermöglicht kleinere Drehgeber. Gleichzeitig erlaubt die hohe Interpolationstiefe von iC-MN eine Erhöhung der Winkelauflösung, oder alternativ, den Einsatz gröberer Maßverkörperungen. (Archiv: Vogel Business Media)

Für eine feine Grundauflösung unterscheidet auch die Nonius-Auswertung Teilungsperioden, verwendet dafür aber weitere Sinussignale anstelle digitaler Absolutcodes. Der Maßverkörperung genügen damit drei an Stelle von bisher mindestens 12 Spuren – Sensor, LED und Linse passen jetzt in viel kleinere Gerätebauformen, die neue Anwendungsfelder erschließen können (Bild 4).

Gleichzeitig bieten aktive Photosensor-Arrays wie iC-LSH hysteresefreie und klirrarme Sinussignale in HiFi-Qualität. Dies ermöglicht eine feinere Interpolation, sodass die Nonius-Auswertung auf einer reduzierten Anzahl von Teilungsperioden basieren kann.

Winkelfehler erkennen und kompensieren

Sensorsignale sind niemals fehlerfrei – für ein besseres Interpolationsergebnis ist es wichtig, relevante Signalfehler zu kennen und zu kompensieren. Typische Fehlerquellen sind ein Offset-behafteter Sensor (OS und OC), eine unterschiedliche Empfindlichkeit zwischen Sinus- und Cosinus-Sensor (Amplituden AS und AC), eine von 90° abweichende Phasenlage zwischen Sinus- und Cosinus-Signal (φSERR bzw. φCERR ) sowie Nichtlinearitäten in der Kennlinie des Sensors (Abweichungen der Sinusform FSIN bzw. FCOS).

Weitere Fehler der Maßverkörperung können hinzukommen, zum Beispiel eine Breitenschwankung der Teilungsperiode, wodurch die Länge der Sinus- bzw. Cosinus-Perioden variiert.

Allgemein lässt sich der Winkel innerhalb einer Teilungsperiode aus dem Arcustangens des Quotienten von Sinus- und Cosinus-Signal gemäß Gleichung 1 berechnen.

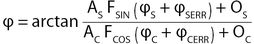
(Gl. 1)

Dieser Winkel wird durch die Interpolationsschaltung quantisiert. Erst aufgrund der Feinunterteilung der Teilungsperiode sind Positionsgeber mit Auflösungen von über 20 Bit pro Umdrehung möglich.